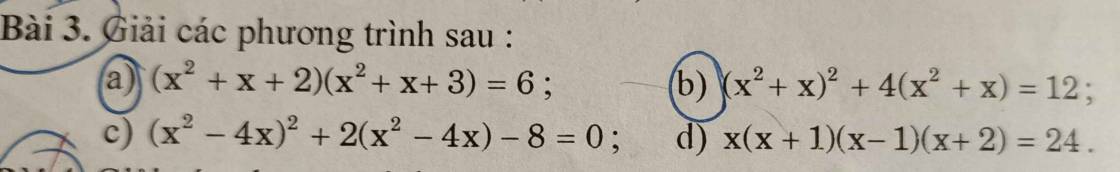a: \(\left(x^2+x+2\right)\left(x^2+x+3\right)=6\)
=>\(\left(x^2+x\right)^2+5\left(x^2+x\right)+6=6\)
=>\(\left(x^2+x\right)^2+5\left(x^2+x\right)=0\)
=>\(\left(x^2+x\right)\left(x^2+x+5\right)=0\)
mà \(x^2+x+5=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}>0\forall x\)
nên \(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
b: \(\left(x^2+x\right)^2+4\left(x^2+x\right)=12\)
=>\(\left(x^2+x\right)^2+4\left(x^2+x\right)-12=0\)
=>\(\left(x^2+x+6\right)\left(x^2+x-2\right)=0\)
=>\(x^2+x-2=0\)
=>(x+2)(x-1)=0
=>\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
c: \(\left(x^2-4x\right)^2+2\left(x^2-4x\right)-8=0\)
=>\(\left(x^2-4x+4\right)\left(x^2-4x-2\right)=0\)
=>\(\left(x-2\right)^2\cdot\left(x^2-4x-2\right)=0\)
=>\(\left[{}\begin{matrix}\left(x-2\right)^2=0\\x^2-4x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\left(x-2\right)^2=6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x-2=\sqrt{6}\\x-2=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\sqrt{6}+2\\x=-\sqrt{6}+2\end{matrix}\right.\)
d: \(x\left(x+1\right)\left(x-1\right)\left(x+2\right)=24\)
=>\(\left(x^2+x\right)\left(x^2+x-2\right)-24=0\)
=>\(\left(x^2+x\right)^2-2\left(x^2+x\right)-24=0\)
=>\(\left(x^2+x-6\right)\left(x^2+x+4\right)=0\)
mà \(x^2+x+4=\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\forall x\)
nên \(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
a) \((x^2+x+2)(x^2+x+3)=6\) (1)
Đặt \(x^2+x+2=t\), khi đó (1) trở thành:
\(t(t+1)=6\\\Leftrightarrow t^2+t-6=0\\\Leftrightarrow t^2-2t+3t-6=0\\\Leftrightarrow t(t-2)+3(t-2)=0\\\Leftrightarrow (t-2)(t+3)=0\\\Rightarrow (x^2+x+2-2)(x^2+x+2+3)=0\\\Leftrightarrow (x^2+x)(x^2+x+5)=0\\\Leftrightarrow x(x+1)\left[\left(x+\frac12\right)^2+\frac{19}{4}\right]=0\\\Leftrightarrow x(x+1)=0\bigg(\text{vì } \left(x+\frac12\right)^2+\frac{19}{4}\ne0;\forall x\bigg)\\\Leftrightarrow \left[\begin{array}{} x=0\\ x+1=0 \end{array} \right.\Leftrightarrow \left[\begin{array}{} x=0\\ x=-1 \end{array} \right.\)
Vậy phương trình đã cho có tập nghiệm là $S=\{0;-1\}$
b) \((x^2+x)^2+4(x^2+x)=12\) (2)
Đặt \(x^2+x=t\), khi đó (2) trở thành:
\(t^2+4t=12\\\Leftrightarrow t^2+4t-12=0\\\Leftrightarrow t^2-2t+6t-12=0\\\Leftrightarrow t(t-2)+6(t-2)=0\\\Leftrightarrow (t-2)(t+6)=0\\\Rightarrow (x^2+x-2)(x^2+x+6)=0\\\Leftrightarrow (x^2-x+2x-2)\left[\left(x+\frac12\right)^2+\frac{23}{4}\right]=0\\\Leftrightarrow x(x-1)+2(x-1)=0\bigg(\text{vì }\left(x+\frac12\right)^2+\frac{23}{4}\ne0;\forall x\bigg)\\\Leftrightarrow (x-1)(x+2)=0\\\Leftrightarrow \left[\begin{array}{} x-1=0\\ x+2=0 \end{array} \right.\Leftrightarrow \left[\begin{array}{} x=1\\ x=-2 \end{array} \right.\)
Vậy phương trình đã cho có tập nghiệm là $S=\{1;-2\}$
$\text{#}Toru$