Bài 1:
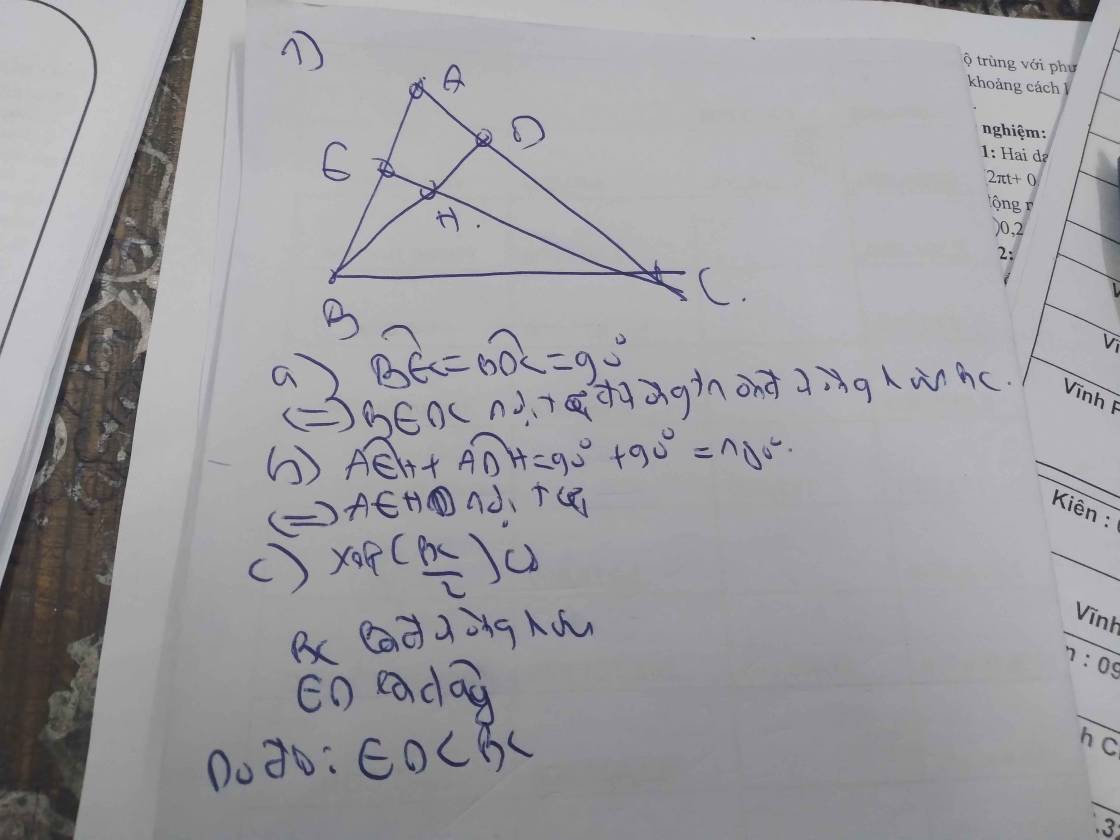
a. Vì $BD, CE$ là đường cao nên $\widehat{BEC}=\widehat{BDC}=90^0$
Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
Hay $B,E,D,C$ cùng thuộc 1 đường tròn.
b. Xét tứ giác $AEHD$ có tổng 2 góc đối nhau $\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0$ nên $AEHD$ là tứ giác nội tiếp
Hay $A,E,H,D$ cùng thuộc 1 đường tròn.
c.
Gọi $I$ là trung điểm $BC$
Xét tam giác $BEC$ vuông tại $E$ nên đường trung tuyến $EI= \frac{BC}{2}=IB=IC$
Tương tự: $DI=IB=IC$
Do đó: $IE=ID=IB=IC$ nên $I$ là tâm đường tròn ngoại tiếp tứ giác $BEDC$
$\Rightarrow BC$ là đường kính
$\Rightarrow BC> ED$
Đúng 1
Bình luận (0)
giúp e bài 3b và bài 6 vs ạ
