Bài 3:
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//MN và DE=MN
Bài 2:
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: EM là đường trung bình của ΔBDC
Suy ra: EM//DC
hay DI//EM
Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay IA=IM

 Giúp e 3 bài này với thực sự cần gấp ạ!!
Giúp e 3 bài này với thực sự cần gấp ạ!!


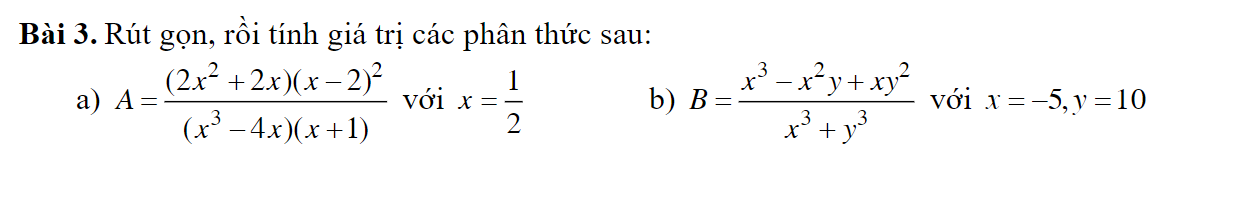
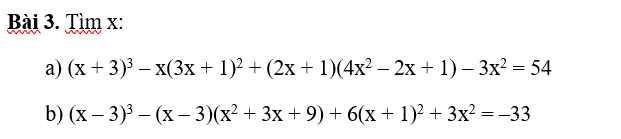 giúp e với đang cần thực sự gấp ạ! e cảm ơnnn
giúp e với đang cần thực sự gấp ạ! e cảm ơnnn







