@ Nguyễn Tuấn Tú bạn không nên bỏ bước phá ngoặc nhé!
Bài 2:
\(H=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+\dfrac{4}{3^4}+...+\dfrac{2017}{3^{2017}}\\ \Rightarrow3H=1+\dfrac{2}{3}+\dfrac{3}{3^2}+\dfrac{4}{3^3}+...+\dfrac{2017}{3^{2016}}\\ \Rightarrow3H-H=\left(1+\dfrac{2}{3}+\dfrac{3}{3^2}+\dfrac{4}{3^3}+...+\dfrac{2017}{3^{2016}}\right)-\left(\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+\dfrac{4}{3^4}+...+\dfrac{2017}{3^{2017}}\right)\\ \Rightarrow2H=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2016}}-\dfrac{2017}{3^{2017}}\)
Đặt \(A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2016}}\)
\(⇒3A=3+1+\dfrac{1}{3}+...+\dfrac{1}{3^{2015}} \)
\(⇒3A-A=(3+1+\dfrac{1}{3}+...+\dfrac{1}{3^{2015}})-(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2016}}) \)
\(\Rightarrow2A=3-\dfrac{1}{3^{2016}}\\\Rightarrow A=\dfrac{3-\dfrac{1}{3^{2016}}}{2}
\)
Thay vào 2H được:
\(2H=\dfrac{3-\dfrac{1}{3^{2016}}}{2}-\dfrac{2017}{3^{2017}}\\
\Rightarrow H=\dfrac{\dfrac{3-\dfrac{1}{3^{2016}}}{2}-\dfrac{2017}{3^{2017}}}{2}=\dfrac{3-\dfrac{1}{3^{2016}}}{4}-\dfrac{2017}{2.3^{2017}}\)
Vậy...
Bài 3:
\(G=\dfrac{3}{5}+\dfrac{3}{5^4}+\dfrac{3}{5^7}+...+\dfrac{3}{5^{100}}\\
\Rightarrow\dfrac{1}{5^3}G=\dfrac{3}{5^4}+\dfrac{3}{5^7}+\dfrac{3}{5^{10}}+...+\dfrac{3}{5^{103}}\\
\Rightarrow G-\dfrac{1}{125}G=\left(\dfrac{3}{5}+\dfrac{3}{5^4}+\dfrac{3}{5^7}+...+\dfrac{3}{5^{100}}\right)-\left(\dfrac{3}{5^4}+\dfrac{3}{5^7}+\dfrac{3}{5^{10}}+...+\dfrac{3}{5^{103}}\right)\\
\Rightarrow\dfrac{124}{125}G=\dfrac{3}{5}-\dfrac{3}{5^{103}}\\
\Rightarrow G=\dfrac{\dfrac{3}{5}-\dfrac{3}{5^{103}}}{\dfrac{124}{125}}\\\Rightarrow G=\dfrac{75}{124}-\dfrac{3}{124.5^{100}}
\)
Vậy...

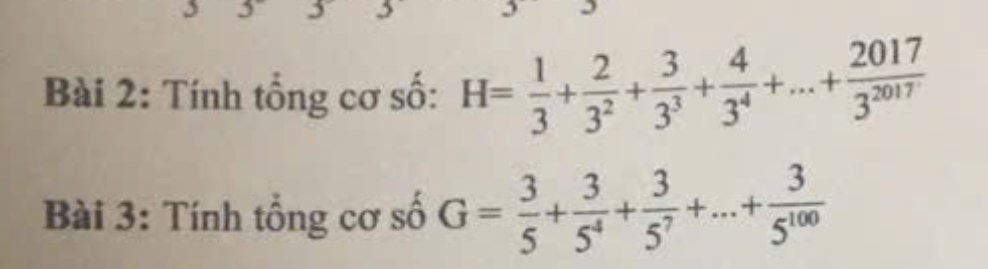








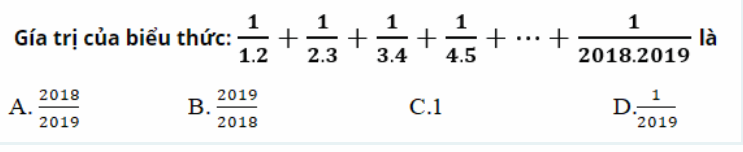




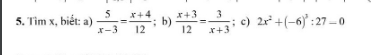


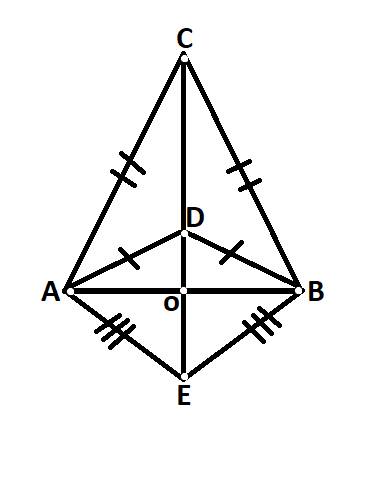

 Giúp em bài này được không ạ! e cảm ơn nhìu ạ
Giúp em bài này được không ạ! e cảm ơn nhìu ạ 

