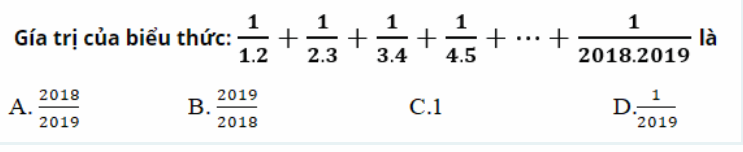9.
Ta có: \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)
\(\Rightarrow\dfrac{1}{n}\left(1+2+...+n\right)=\dfrac{1}{n}.\dfrac{n\left(n+1\right)}{2}=\dfrac{n+1}{2}\)
Áp dụng:
\(C=-\dfrac{3+1}{2}-\dfrac{4+1}{2}-...-\dfrac{50+1}{2}\)
\(=-\dfrac{4}{2}-\dfrac{5}{2}-...-\dfrac{51}{2}\)
\(=-\left(\dfrac{4+5+...+51}{2}\right)\)
\(=-\left(\dfrac{1+2+...+51-\left(1+2+3\right)}{2}\right)\)
\(=-\left(\dfrac{\dfrac{51.\left(51+1\right)}{2}-6}{2}\right)=-660\)
10.
Ta có:
\(1+2+..+n=\dfrac{n\left(n+1\right)}{2}\)
\(\Rightarrow\dfrac{1}{1+2+...+n}=\dfrac{2}{n\left(n+1\right)}\)
\(\Rightarrow1-\dfrac{1}{1+2+...+n}=1-\dfrac{2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
Áp dụng:
\(E=\dfrac{\left(2-1\right)\left(2+2\right)}{2\left(2+1\right)}.\dfrac{\left(3-1\right)\left(3+2\right)}{3\left(3+1\right)}...\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}...\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}=\dfrac{1.2...\left(n-1\right)}{2.3...n}.\dfrac{4.5...\left(n+2\right)}{3.4...\left(n+1\right)}\)
\(=\dfrac{1}{n}.\dfrac{n+2}{3}=\dfrac{n+2}{3n}\)
\(\Rightarrow\dfrac{E}{F}=\dfrac{n+2}{3n}:\dfrac{n+2}{n}=\dfrac{n+2}{3n}.\dfrac{n}{n+2}=\dfrac{1}{3}\)

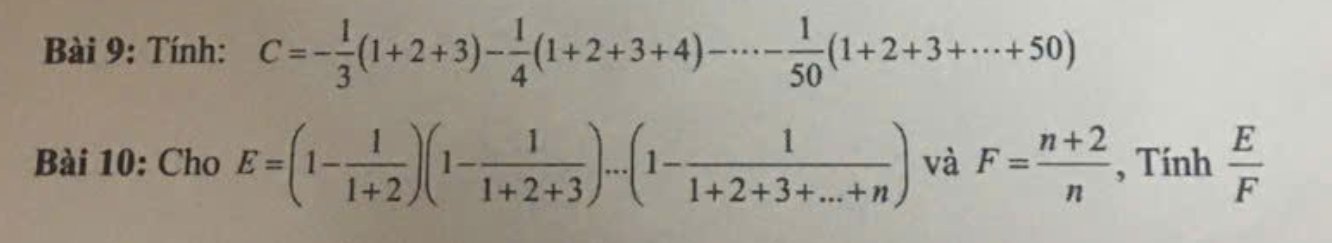






 Giúp em bài này được không ạ! e cảm ơn nhìu ạ
Giúp em bài này được không ạ! e cảm ơn nhìu ạ