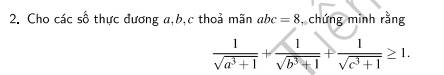Lời giải:
Gọi vận tốc lúc đầu là $a$ km/h và thời gian dự định là $b$ giờ
.Ta có:
$AB=ab=(a+3)(b-2)=(a-2)(b+3)$
$\Leftrightarrow ab=ab-2a+3b-6=ab+3a-2b-6$
$\Leftrightarrow -2a+3b=6$ và $3a-2b=6$
$\Rightarrow a=6; b=6$
$\Rightarrow AB=ab=6.6=36$ (km)
Bài 3:
Gọi thời gian dự định đi quãng đường AB là $t$ (giờ)
Theo bài ra ta có:
$AB=45(t-1)=30(t+1)$
$\Rightarrow t=5$ (giờ)
$AB=45(5-1)=45.4=180$ (km)
Thời điểm người đó xuất phát: $10-5=5$ (giờ)
Bài 3:
Gọi thời gian người đó đi hết quãng đường AB là x(giờ)
(Điều kiện: x>0)
KHi xe chạy với vận tốc 45km/h thì xe đến sớm 1 giờ nên độ dài quãng đường AB khi xe chạy với vận tốc 45km/h là:
45(x-1)(km)
Khi xe chạy với vận tốc 30km/h thì xe đến muộn 1 giờ nên độ dài quãng đường AB khi xe chạy với vận tốc 30km/h là:
30(x+1)(km)
Do đó, ta có phương trình:
45(x-1)=30(x+1)
=>3(x-1)=2(x+1)
=>3x-3=2x+2
=>3x-2x=3+2
=>x=5(nhận)
Độ dài quãng đường AB là:
45(x-1)=45*(5-1)=45*4=180(km)
Thời điểm người đó xuất phát là:
10-5=5(giờ)
Bài 4:
Gọi vận tốc dự định và thời gian dự định của cano để đi hết quãng đường AB lần lượt là a(km/h) và b(h)
(Điều kiện: a>0 và b>0)
Nếu tăng vận tốc thêm 3km/h thì đến sớm hơn 2 giờ so với dự kiến nên độ dài quãng đường AB khi cano đi nhanh hơn 3km/h so với vận tốc dự định là:
(a+3)(b-2)=ab-2a+3b-6=ab
=>-2a+3b-6=0
=>-2a+3b=6
=>2a-3b=-6(1)
Nếu giảm vận tốc đi 2km/h thì cano sẽ đến muộn hơn 3 giờ nên độ dài quãng đường AB khi cano đi chậm hơn dự kiến 2km/h là:
ab=(a-2)(b+3)
=>ab=ab+3a-2b-6
=>3a-2b-6=0
=>3a-2b=6(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a-3b=-6\\3a-2b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-9b=-18\\6a-4b=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-5b=-30\\3a-2b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\3a=2b+6=2\cdot6+6=12+6=18\end{matrix}\right.\)
=>b=6 và a=6
Độ dài khoảng cách giữa hai bến là:
6*6=36(km)









 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 





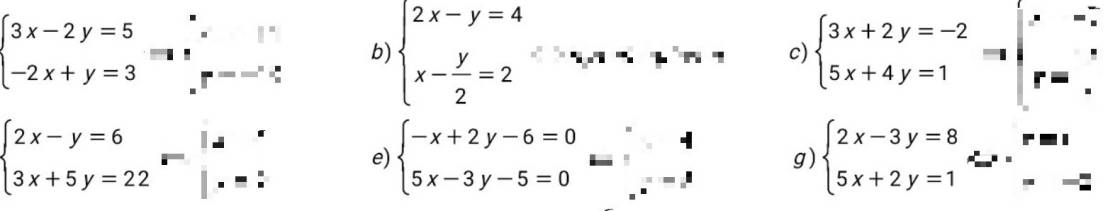
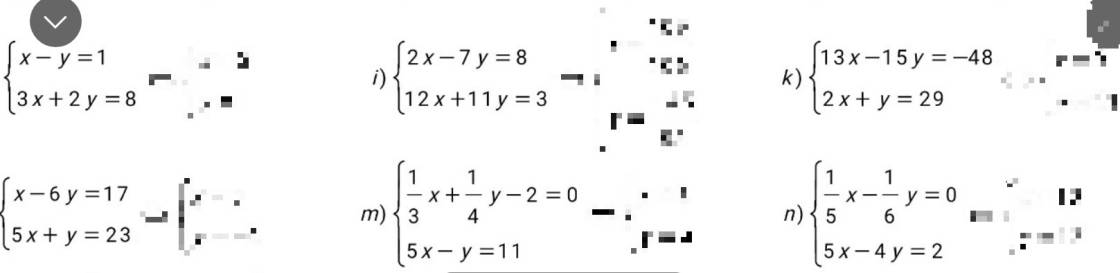 giúp mik với mik đg cần gấp
giúp mik với mik đg cần gấp