a: \(\left|\dfrac{1}{2}x\right|=3-2x\)
=>\(\dfrac{1}{2}\left|x\right|=3-2x\)
=>\(\left|x\right|=\left(3-2x\right)\cdot2=6-4x\)
=>\(\left\{{}\begin{matrix}6-4x>=0\\\left(6-4x\right)^2=x^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x< =6\\\left(6-4x-x\right)\left(6-4x+x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(6-5x\right)\left(6-3x\right)=0\end{matrix}\right.\Leftrightarrow x=\dfrac{6}{5}\)
b: |x-1|=3x+2
=>\(\left\{{}\begin{matrix}3x+2>=0\\\left(3x+2\right)^2=\left(x-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{2}{3}\\\left(3x+2-x+1\right)\left(3x+2+x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{2}{3}\\\left(2x+3\right)\left(4x+1\right)=0\end{matrix}\right.\Leftrightarrow x=-\dfrac{1}{4}\)
c: |5x|=x-12
=>\(\left\{{}\begin{matrix}x-12>=0\\\left(5x\right)^2=\left(x-12\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=12\\\left(5x-x+12\right)\left(5x+x-12\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=12\\\left(4x+12\right)\left(6x-12\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=12\\x\in\left\{-3;2\right\}\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
d: |7-x|=5x+1
=>|x-7|=5x+1
=>\(\left\{{}\begin{matrix}5x+1>=0\\\left(5x+1\right)^2=\left(x-7\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{5}\\\left(5x+1-x+7\right)\left(5x+1+x-7\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{5}\\\left(4x+8\right)\left(6x-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{5}\\x\in\left\{-2;1\right\}\end{matrix}\right.\Leftrightarrow x=1\)
Giải chi tiết giúp mình nhé
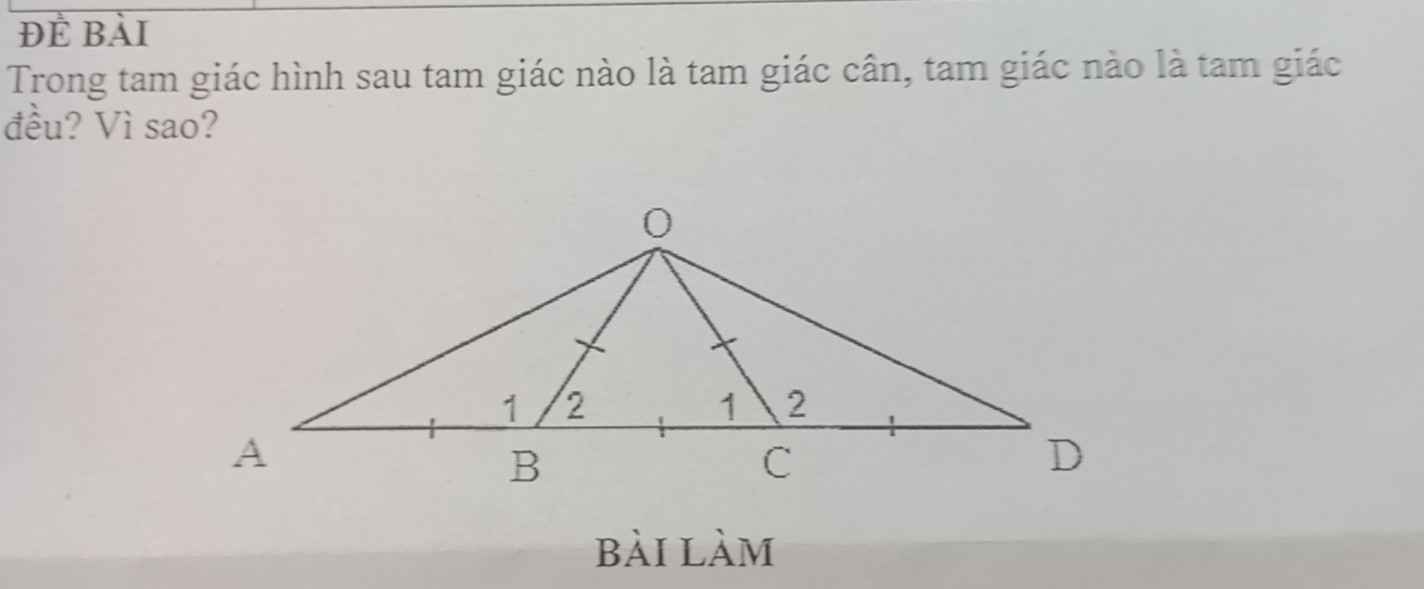
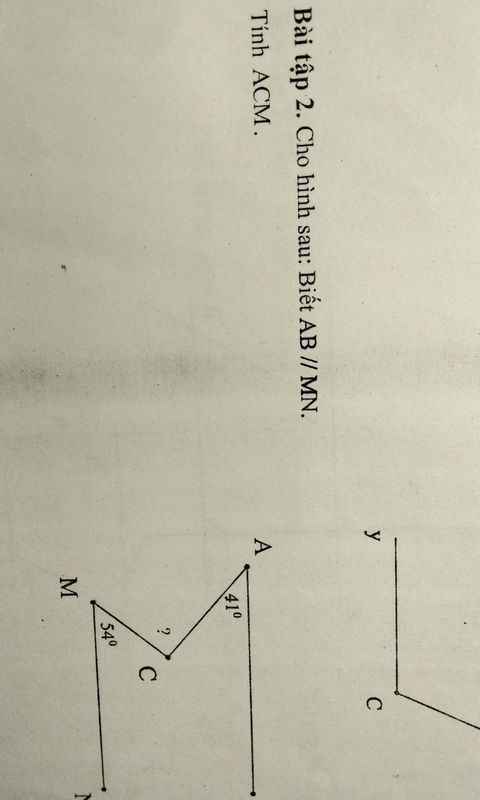
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
