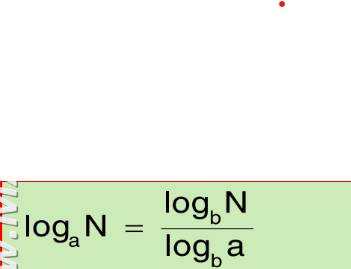\(y=\log_2\left(x^2-3x+2\right)\)
Hàm số xác định khi và chỉ khi
\(x^2-3x+2>0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)>0\)
\(\Leftrightarrow x< 1\cup x>2\)
\(D=\left(-\infty;1\right)\cup\left(2;+\infty\right)\)
\(y'=\dfrac{2x-3}{\ln_2\left(x^2-3x+2\right)}\)
Để hàm số nghịch biến \(y'< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3< 0\\x^2-3x+2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{3}{2}\\x< 1\cup x>2\end{matrix}\right.\) \(\)
\(\Leftrightarrow x< 1\) hay \(x\in\left(-\infty;1\right)\)
Nên chọn C
Đúng 1
Bình luận (0)
