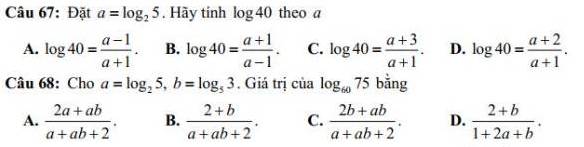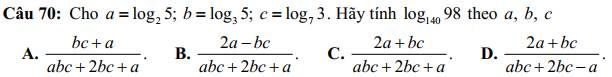Câu 67: \(\log40=\log\left(2^3\cdot5\right)=\log2^3+\log5\)
\(=3\cdot\log2+\log5\)
\(3\cdot\log_2=\frac{3}{\log_210}=\frac{3}{\log_2\left(2\cdot5\right)}=\frac{3}{1+\log_25}=\frac{3}{1+a}\)
\(\log40=\frac{\log_240}{\log_210}=\frac{\log_2\left(2^3\cdot5\right)}{\log_2\left(2\cdot5\right)}=\frac{3+\log_25}{1+\log_25}\)
\(=\frac{a+3}{a+1}\)
=>Chọn C
Câu 70: \(a=\log_25\)
=>\(\frac{1}{a}=\log_52\)
\(b=\log_35\)
=>\(\frac{1}{b}=\log_53\)
\(c=\log_73\)
\(\log_53=\log_5\left(7^{\log_73}\right)=\log_57\cdot\log_73=c\cdot\log_57\)
=>\(\log_57=\frac{\log_53}{c}=\frac{1}{bc}\)
\(\log_{140}98=\frac{\log_598}{\log_5140}=\frac{\log_5\left(2\cdot7^2\right)}{\log_5\left(5\cdot7\cdot2^2\right)}=\frac{\log_52+2\cdot\log_57}{1+\log_57+\log_54}\)
\(=\frac{\frac{1}{a}+\frac{2}{bc}}{2\cdot\frac{1}{a}+1+\frac{1}{bc}}=\frac{bc+2a}{abc}:\left(\frac{2}{a}+1+\frac{1}{bc}\right)\)
\(=\frac{bc+2a}{abc}:\frac{2bc+abc+a}{abc}=\frac{bc+2a}{2bc+abc+a}\)
=>Chọn C