Question

giải tam giác ABC vuông tại C biết BC=20cm,góc A=30 độ

Answer 1

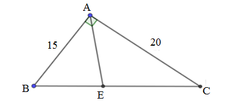
ΔCAB vuông tại C

=>\(\widehat{A}+\widehat{B}=90^0\)

=>\(\widehat{B}=90^0-30^0=60^0\)

Xét ΔABC vuông tại C có \(sinA=\dfrac{BC}{AB}\)

=>\(\dfrac{20}{AB}=sin30=\dfrac{1}{2}\)

=>AB=40(cm)

ΔABC vuông tại C

=>\(CA^2+CB^2=AB^2\)

=>\(CA^2=40^2-20^2=1200=\left(20\sqrt{3}\right)^2\)

=>\(CA=20\sqrt{3}\left(cm\right)\)

Answer 2

xét`ΔABC` vuông tại `C` có :

\(AC=\cot30^0\cdot20=\sqrt{3}\cdot20=20\sqrt{3}\)

`AC^2 + CB^2 = AB^2`

`=> `\(\left(20\sqrt{3}\right)^2+20^2=AB^2\)

`=>`\(AB^2=1600\)

`=> AB = 40`

Có :

\(\widehat{A}+\widehat{B}=90^0\)

=>`\(\widehat{B}=90^0-\widehat{A}=90^0-30^0=60^0\)