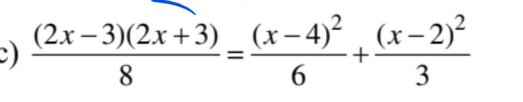\(\dfrac{\left(2x-3\right)\left(2x+3\right)}{8}=\dfrac{\left(x-4\right)^2}{6}+\dfrac{\left(x-2\right)^2}{3}\)
=>\(\dfrac{4x^2-9}{8}=\dfrac{\left(x-4\right)^2+2\left(x-2\right)^2}{6}\)
=>\(\dfrac{3\left(4x^2-9\right)}{24}=\dfrac{4\left(x^2-8x+16+2x^2-8x+8\right)}{24}\)
=>\(3\left(4x^2-9\right)=4\left(3x^2-16x+24\right)\)
=>\(12x^2-27=12x^2-64x+96\)
=>-64x=-27-96=-123
=>\(x=\dfrac{123}{64}\)
` (2x-3)(2x+3) = 4x^2 -9 `
\(\dfrac{4x^2-9}{8}\)
\(\dfrac{x^2 - 8x + 16}{6} + \dfrac{x^2 - 4x + 4}{3}\)
\(24. \dfrac{4x^2 - 9}{8} = 24 . ( \dfrac{x^2 - 8x + 16 }{6} + \dfrac{x^2 - 4x + 4}{3})\)
` 3(4x^2 - 9) = 4(x^2-8x + 16) + 8 ( x^2 - 4x + 4) `
` 12x^2 - 27 = 4x^2 - 32x + 64 + 8x^2 - 32x + 32 `
` 12x^2 - 27 = 12x^2 - 64x + 96 `
` 12x^2 - 12x^2 + 64x = 96 + 27 `
` 64x = 123 `
` => x = 123/64 `