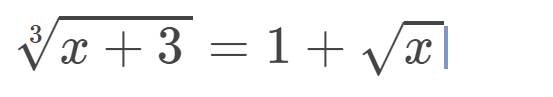Question

giải pt 

Answer 1

Lời giải:
ĐKXĐ: $x\geq 0$

Đặt $\sqrt[3]{x+3}=a; \sqrt{x}=b(a,b\geq 0)$. Khi đó ta có:

\(\left\{\begin{matrix} a=1+b\\ a^3-b^2=3\end{matrix}\right.\Rightarrow (b+1)^3-b^2=3\)

$\Leftrightarrow b^3+2b^2+3b-2=0$

Sử dụng công thức nghiệm Cardano cho pt bậc 3 suy ra 

\(b=\frac{1}{3}(-2-\frac{5}{\sqrt[3]{46+3\sqrt{249}}}+\sqrt[3]{46+3\sqrt{249}})\)

\(\Rightarrow x=\frac{1}{3}(-2-\frac{47}{\sqrt[3]{199+24\sqrt{249}}}+\sqrt[3]{199+24\sqrt{249}})\)