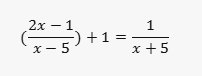\(\dfrac{2x-1}{x-5}+1=\dfrac{1}{x+5}\)(ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
=>\(\dfrac{2x-1+x-5}{x-5}=\dfrac{1}{x+5}\)
=>\(\dfrac{3x-6}{x-5}=\dfrac{1}{x+5}\)
=>\(\left(3x-6\right)\left(x+5\right)=x-5\)
=>\(3x^2+15x-6x-30-x+5=0\)
=>\(3x^2+8x-25=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{-4+\sqrt{91}}{3}\left(nhận\right)\\x=\dfrac{-4-\sqrt{91}}{3}\left(nhận\right)\end{matrix}\right.\)
` (2x-1)/(x-5) + 1 = 1/(x+5)`
`=> ( x-5 + 2x -1 )/(x-5) = 1/(x+5)`
`=> (3x-6)/(x-5) = 1/(x+5)`
`=> (3x-6)(x+5) = x-5`
`=> -6x - 30 + 3x^2 + 15x = x-5`
`=> -6x - 30 + 3x^2 + 15x - x + 5 = 0`
`=> 8x - 25 + 3x^2 = 0`
`=>` \(\left[{}\begin{matrix}\dfrac{-4+\sqrt{91}}{3}\left(n\right)\\\dfrac{-4-\sqrt{91}}{3}\left(n\right)\end{matrix}\right.\)
Vậy...