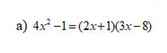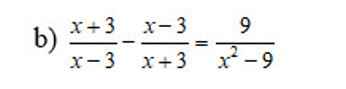\(\Leftrightarrow\left(2x+1\right)\left(3x-8\right)-\left(2x+1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(3x-8-2x+1\right)=0\)
=>(2x+1)(x-7)=0
=>x=7 hoặc x=-1/2
a) \(4x^2-1=\left(2x+1\right)\left(3x-8\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-8\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+8\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(7-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\7-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=7\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{-1}{2};7\)