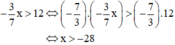\(\dfrac{1}{1}+\dfrac{1}{3}+...+\dfrac{1}{2023}-\left(\dfrac{1}{1013}+\dfrac{1}{1014}+...+\dfrac{1}{2024}\right)\cdot x=\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2024}\)
=>\(x\left(\dfrac{1}{1013}+\dfrac{1}{1014}+...+\dfrac{1}{2024}\right)=1+\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2}-\dfrac{1}{4}-...-\dfrac{1}{2024}\)
=>\(x\left(\dfrac{1}{1013}+\dfrac{1}{1014}+...+\dfrac{1}{2024}\right)=1+\dfrac{1}{2}+...+\dfrac{1}{2024}-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2024}\right)\)
=>\(x\left(\dfrac{1}{1013}+\dfrac{1}{1014}+...+\dfrac{1}{2024}\right)=\dfrac{1}{1013}+\dfrac{1}{1014}+...+\dfrac{1}{2024}\)
=>x=1








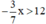 . Ta có:
. Ta có: