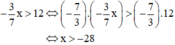\(\dfrac{5-x}{4x^2-8x}+\dfrac{7}{8}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8x-16}\)
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}-\dfrac{x-1}{2x\left(x-2\right)}-\dfrac{1}{8\left(x-2\right)}+\dfrac{7}{8}=0\)
\(\Leftrightarrow\dfrac{2\left(5-x\right)-4\left(x-1\right)-x+7x}{8x\left(x-2\right)}=0\)
\(\Leftrightarrow10-x-4x+4-x+7x=0\)
\(\Leftrightarrow x+14=0\)
\(\Leftrightarrow x=-14\)
Vậy \(S=\left\{-14\right\}\)

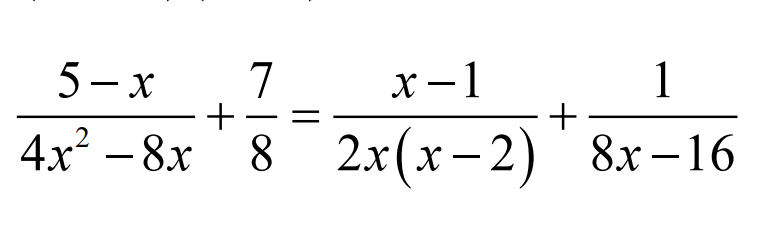





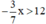 . Ta có:
. Ta có: