(Điều kiện : x – 15º ≠ 90º + k.180º với ∀ k ∈ Z)
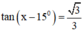
⇔ x – 15º = 30º + k180º , k ∈ Z
⇔ x = 45º + k.180º, k ∈ Z
Vậy phương trình có họ nghiệm x = 45º + k.180º (k ∈ Z).
(Điều kiện : x – 15º ≠ 90º + k.180º với ∀ k ∈ Z)
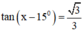
⇔ x – 15º = 30º + k180º , k ∈ Z
⇔ x = 45º + k.180º, k ∈ Z
Vậy phương trình có họ nghiệm x = 45º + k.180º (k ∈ Z).
1) cho góc x thỏa mãn \(cosx=-\dfrac{4}{5}\) và \(\pi< x< \dfrac{3\pi}{2}\) tính \(P=tan\left(x-\dfrac{\pi}{4}\right)\)
2) giải phương trình \(2cosx-\sqrt{2}=0\)
3) phương trình lượng giác \(cos3x=cos\dfrac{\pi}{15}\) có nghiệm là
Giải phương trình sau:
\(\tan\left(x+\dfrac{\pi}{3}\right)+\cot\left(\dfrac{\pi}{2}-3x\right)=0\)
Giải phương trình 3 . tan x - 3 = 0
![]()
![]()
![]()
![]()
a) Giải phương trình trên tập số thực:
\(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
b) Giải hệ phương trình sau:
\(\left\{{}\begin{matrix}x^2+2x\sqrt{xy}=y^2\sqrt{y}\\\left(4x^3+y^3+3x^2\sqrt{x}\right)\left(15\sqrt{x}+y\right)=3\sqrt{x}\left(y\sqrt{y}+x\sqrt{y}+4x\sqrt{x}\right)^2\end{matrix}\right.\) ; với \(x,y\inℝ\)
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)
Giải phương trình sau: tan x - c o t x = 3 2
![]()
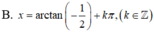
![]()
![]()
Giải phương trình sau: tanx + tan (x+π/4) = 1
Phương trình tanx + tan(x + π 3 ) + tan(x + 2 π 3 ) = 3 3 tương đương với phương trình.
A. cot x = 3
B. cot 3x = 3
C. tan x = 3
D. tan 3x = 3
Giải phương trình sau: tan(2x + 1).tan(3x – 1) = 1
Giải phương trình sau: 1 sin 2 x = c o t x + 3
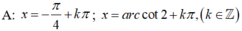
![]()

![]()