Question

giải kĩ giúp ạ

Answer 1

4.

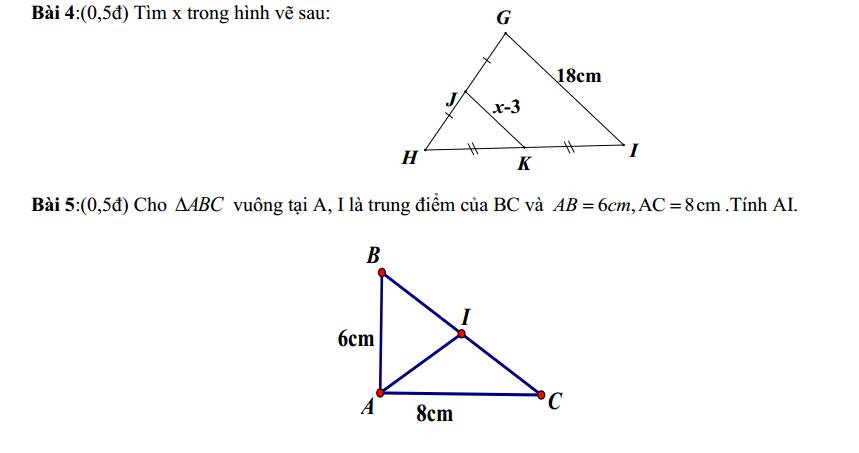
Từ hình vẽ ta thấy J là trung điểm HG, K là trung điểm HI

\(\Rightarrow JK\) là đường trung bình tam giác HGI

\(\Rightarrow JK=\dfrac{1}{2}GI\)

\(\Rightarrow x-3=\dfrac{1}{2}.18=9\)

\(\Rightarrow x=12\left(cm\right)\)

5.

Áp dụng định lý Pitago:

\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)

Do I là trung điểm BC \(\Rightarrow AI\) là đường trung tuyến ứng với cạnh huyền

\(\Rightarrow AI=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)

Answer 2

Do J là trung điểm của HG, K là trung điểm của HI (gt) nên JK là đường trung bình của tam giác HGI. Khi đó \(JK=\dfrac{IG}{2}\Leftrightarrow x-3=\dfrac{18}{2}\Leftrightarrow x=12\)