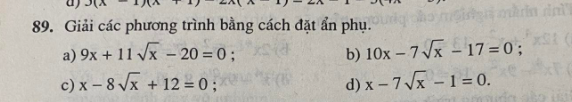c: \(\Leftrightarrow\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-6\right)=0\)
=>x=4 hoặc x=36
d: Đặt \(\sqrt{x}=a\)
Pt sẽ là \(a^2-a-7=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-7\right)=29>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{1-\sqrt{29}}{2}\left(loại\right)\\a_2=\dfrac{1+\sqrt{29}}{2}\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{x}=\dfrac{\sqrt{29}+1}{2}\)
hay \(x=\dfrac{30+2\sqrt{29}}{4}=\dfrac{15+\sqrt{29}}{2}\)
c) Đặt \(\sqrt{x}=a\left(a\ge0\right)\)
Ta có PT
\(a^2-8a+12=0\)
\(\Delta=\left(-8\right)^2-4.12=64-48=16>0\)
PT có 2 nghiệm phân biệt
\(\left[{}\begin{matrix}a_1=\dfrac{8+\sqrt{16}}{2}=\dfrac{12}{2}=6\\a_2=\dfrac{8-\sqrt{16}}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
Ta có
Với a = 6 thì \(\sqrt{x}=6\Leftrightarrow x=36\left(tm\right)\)
Với a = 2 thì \(\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)