\(g.\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(x\ne3;x\ne-1\right)\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow x^2+x+x^2-3x=4x\)
\(\Leftrightarrow2x^2-6x=0\)
\(\Leftrightarrow2x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=3\left(ktm\right)\end{matrix}\right.\)
g) \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
ĐKXĐ: \(x\ne-1;x\ne3\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)+x\left(x-3\right)}{2\left(x-3\right)\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x^2+x+x^2-3x}{2\left(x-3\right)\left(x+1\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow2x^2-2x=4x\)
\(\Leftrightarrow2x^2-6x=0\)
\(\Leftrightarrow2x\left(x-3\right)=0\)
\(\left[{}\begin{matrix}2x=0\\x-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\left(n\right)\\x=3\left(l\right)\end{matrix}\right.\)
Vậy \(x=0\)
h) \(5+\dfrac{76}{x^2-16}=\dfrac{2x-1}{x+4}-\dfrac{3x-1}{4-x}\)
ĐKXĐ: \(x\ne\pm4\)
\(\Leftrightarrow\dfrac{5\left(x^2-16\right)+76}{x^2-16}=\dfrac{\left(2x-1\right)\left(x-4\right)+\left(3x-1\right)\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow\dfrac{5x^2-80+76}{x^2-16}=\dfrac{2x^2-9x+4+3x^2+11x-4}{x^2-16}\)
\(\Leftrightarrow5x^2-4=5x^2+2x\)
\(\Leftrightarrow2x=-4\)
\(\Leftrightarrow x=-2\left(n\right)\)
Vậy \(x=-2\)
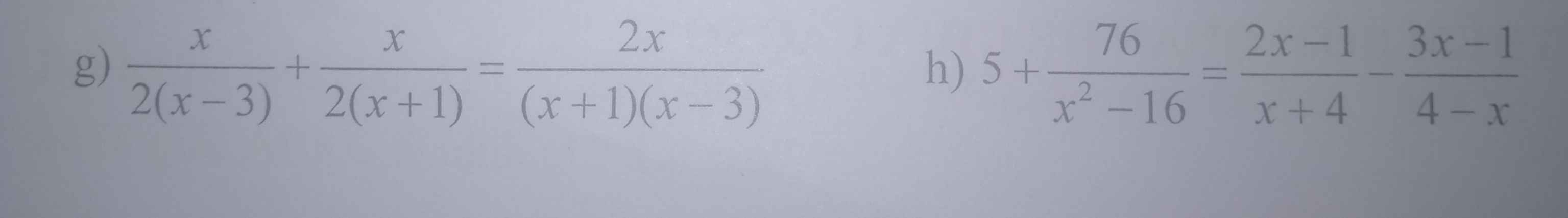
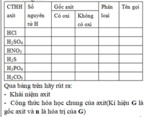
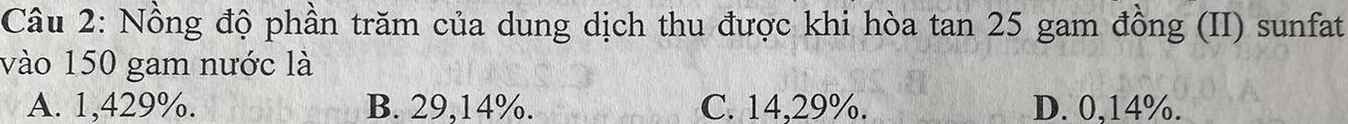giải chi tiết giúp mình với ạ!!!!!!!!!