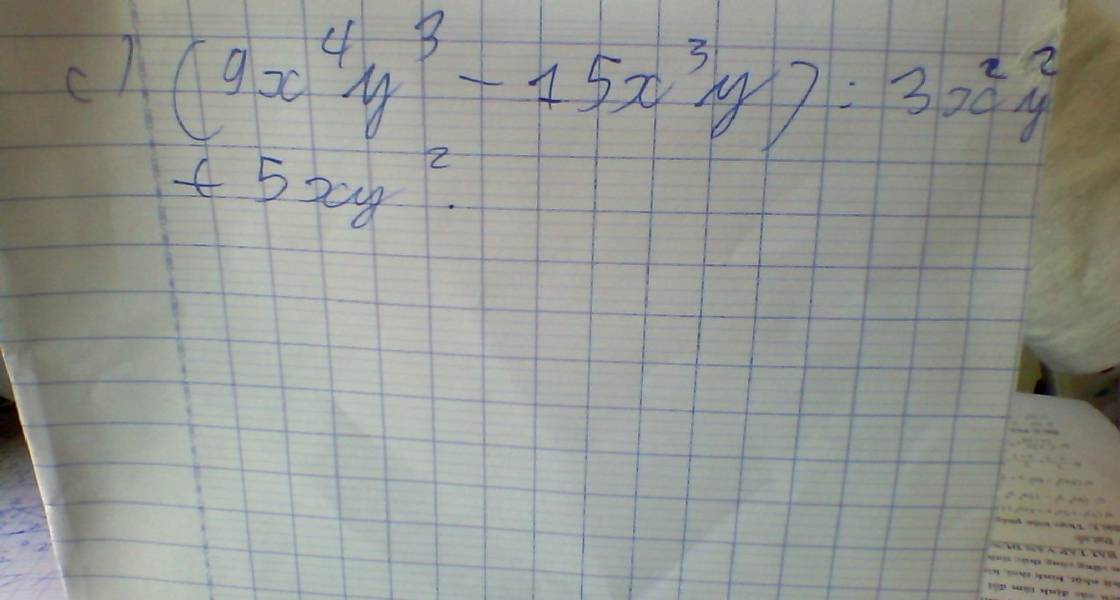5:
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng vơi ΔHAC
=>AB/HA=BC/AC
=>AB*AC=AH*CB
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=4/8=0,5
=>AD=1,5cm; CD=2,5cm
BH=3^2/5=1,8cm
=>AH=2,4cm
AE/AB=EH/BH
=>AE/3=EH/1,8=(AE+EH)/(3+1,8)=0,5
=>AE=1,5cm; HE=0,9cm
\(S_{BHE}=\dfrac{1}{2}\cdot1.8\cdot0.9=0.81\left(cm^2\right)\)
\(S_{ABD}=\dfrac{1}{2}\cdot BA\cdot AD=\dfrac{1}{2}\cdot3\cdot1.5=2.25\left(cm^2\right)\)
=>\(\dfrac{S_{BHE}}{S_{ABD}}=\dfrac{81}{225}=\dfrac{9}{25}\)