Bài 19:
a: ΔOBC cân tại O
mà OM là đường cao
nên M là trung điểm của BC
Xét tứ giác OBAC có
M là trung điểm chung của AO và BC
=>OBAC là hình bình hành
Hình bình hành OBAC có OB=OC
nên OBAC là hình thoi
b: OBAC là hình thoi
=>OB=BA
mà OB=OA
nên OB=OA=BA
=>ΔOBA đều
=>\(\hat{BOA}=60^0\)
Xét ΔOBE vuông tại B có tan BOE\(=\frac{BE}{OB}\)
=>\(\frac{BE}{R}=\tan60=\sqrt3\)
=>\(BE=R\sqrt3\)
Bài 18:
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(\hat{BAC}=90^0\)
b: Xét (I) có
ΔAHO nội tiếp
AO là đường kính
Do đó: ΔAHO vuông tại H
=>OH⊥AB tại H
Xét (I) có
ΔAKO nội tiếp
AO là đường kính
Do đó: ΔAKO vuông tại K
=>OK⊥AC tại K
Xét tứ giác AHOK có \(\hat{AHO}=\hat{AKO}=\hat{HAK}=90^0\)
nên AHOK là hình chữ nhật
=>AO cắt HK tại trung điểm của mỗi đường
mà I là trung điểm của AO
nên I là trung điểm của HK
=>H,I,K thẳng hàng
c: ΔOBA cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOB
ΔOAC cân tại O
mà OK là đường cao
nên OK là phân giác của góc COA
Xét ΔOAD và ΔOBD có
OA=OB
\(\hat{AOD}=\hat{BOD}\)
OD chung
Do đó: ΔOAD=ΔOBD
=>DA=DB
Xét ΔOAE và ΔOCE có
OA=OC
\(\hat{AOE}=\hat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>EA=EC
BD+EC
=DA+EA
=DE
d: AHOK là hình chữ nhật
=>\(\hat{HOK}=90^0\)
=>\(\hat{DOE}=90^0\)
=>O nằm trên đường tròn đường kính DE
Gọi K là trung điểm của DE
=>O,D,E cùng nằm trên (K)
Xét hình thang BDEC có
O,K lần lượt là trung điểm của BC,DE
=>OK là đường trung bình của hình thang BDEC
=>OK//BD//EC
=>OK⊥BC tại O
Xét (K) có
KO là bán kính
BC⊥KO tại O
Do đó: BC là tiếp tuyến tại O của (K)
hay BC là tiếp tuyến của đường tròn đường kính DE
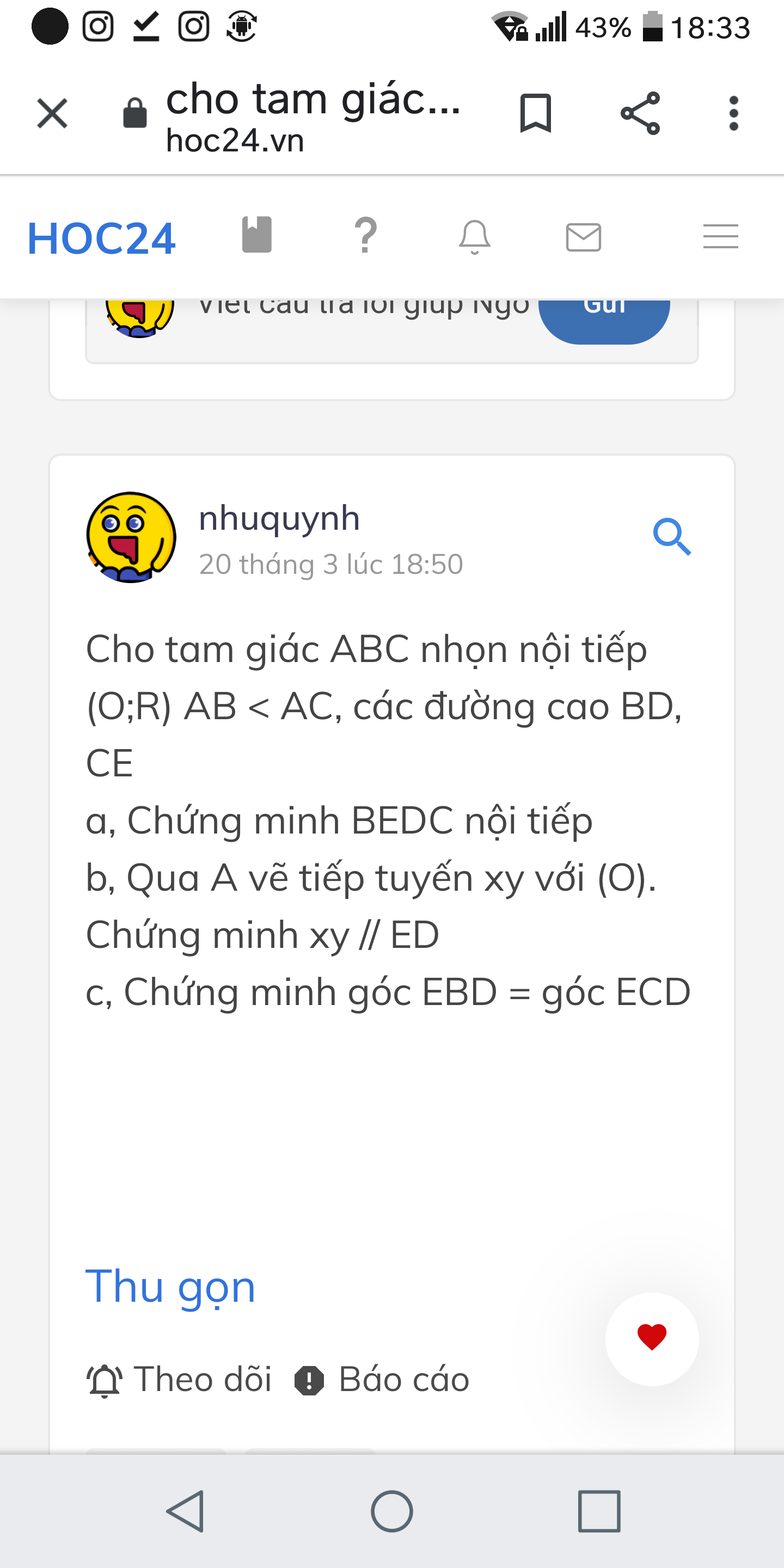
giải giúp mình vs ạ !
giải giúp mình vs ạ !
giải giúp mình vs ạ !
