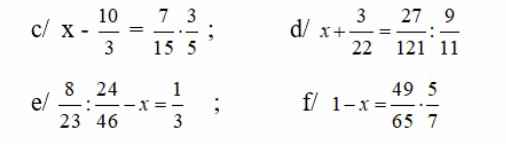gọi O là tâm đường tròn đường kính AD
\(=>OB=AO=OD=\dfrac{AD}{2}=\dfrac{8}{2}=4cm\)
\(\Delta ABO=\Delta BCO\left(c.c.c\right)\) (do AB=BC, OB chung, OA=OC=R)
\(=>\)góc O1= góc O2=>OM phân giác
mà \(\Delta OAC\) cân tại O=>OM là đường trung trực
\(=>AM=MC\) mà \(OA=OD=R\)\(=>OM\) là đường trung bình tam giác ACD=>\(OM=\dfrac{1}{2}CD\)
theo pytago\(=>OA^2-OM^2=AB^2-BM^2\)
\(< =>4^2-OM^2=2^2-\left(OB-OM\right)^2\)
\(< =>16^{ }-OM^2=4-\left(4-OM\right)^2=>OM=3,5=>CD=7cm\)











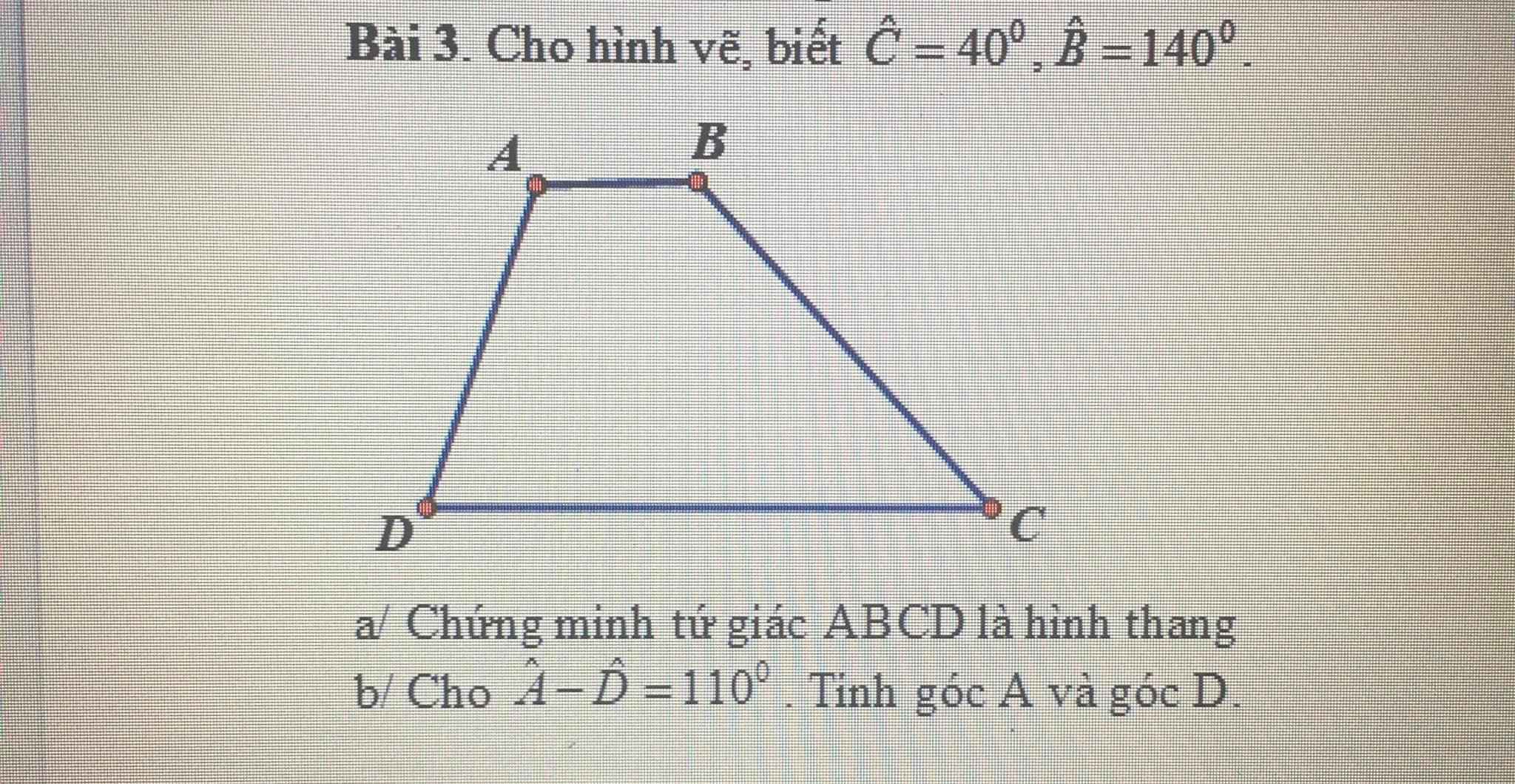





 ai giải giúp mình với ạ mình cảm ơn
ai giải giúp mình với ạ mình cảm ơn