a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
a) Xét tứ giác BDEC có
\(\widehat{BDC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BDC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BDEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: BDEC là tứ giác nội tiếp(cmt)
nên \(\widehat{DEB}=\widehat{DCB}\)(hai góc nội tiếp cùng chắn cung BD)
hay \(\widehat{KEB}=\widehat{KCD}\)
Xét ΔKEB và ΔKCD có
\(\widehat{KEB}=\widehat{KCD}\)(cmt)
\(\widehat{DKB}\) chung
Do đó: ΔKEB\(\sim\)ΔKCD(g-g)
Suy ra: \(\dfrac{KE}{KC}=\dfrac{KB}{KD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(KD\cdot KE=KB\cdot KC\)(đpcm)

 giải giúp mình với, cảm ơn nhiều
giải giúp mình với, cảm ơn nhiều





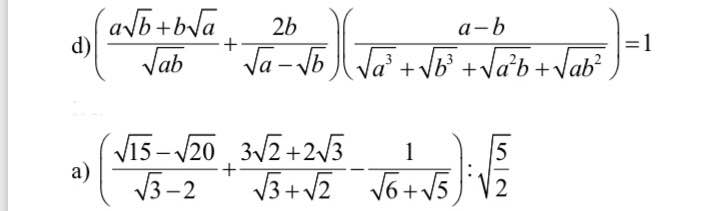



 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
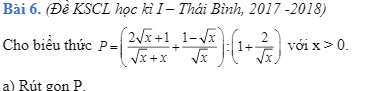





 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.
