a: Ta có: ABCD là hình thang cân
=>\(\hat{DAB}=\hat{CBA};\hat{ADC}=\hat{DCB}\)
Ta có: \(\hat{DAB}+\hat{CBA}=\frac12\left(\hat{ADC}+\hat{DCB}\right)\)
=>\(2\cdot\hat{CBA}=\frac12\cdot2\cdot\hat{DCB}\)
=>\(\hat{DCB}=2\cdot\hat{CBA}\)
Ta có: DC//AB
=>\(\hat{DCB}+\hat{CBA}=180^0\) (hai góc trong cùng phía)
=>\(2\cdot\hat{CBA}+\hat{CBA}=180^0\)
=>\(3\cdot\hat{CBA}=180^0\)
=>\(\hat{CBA}=60^0\)
=>\(\hat{DAB}=\hat{CBA}=60^0\)
Ta có: \(\hat{DCB}=2\cdot\hat{CBA}\)
=>\(\hat{DCB}=2\cdot60^0=120^0\)
Ta có: \(\hat{DCB}=\hat{CDA}\)
mà \(\hat{DCB}=120^0\)
nên \(\hat{CDA}=120^0\)
b: ΔCAB vuông tại C
=>\(\hat{CAB}+\hat{CBA}=90^0\)
=>\(\hat{CAB}=90^0-60^0=30^0\)
Ta có: \(\hat{DAC}+\hat{CAB}=\hat{DAB}\) (tia AC nằm giữa hai tia AD và AB)
=>\(\hat{DAC}=60^0-30^0=30^0\)
=>\(\hat{DAC}=\hat{BAC}\)
=>AC là phân giác của góc BAD










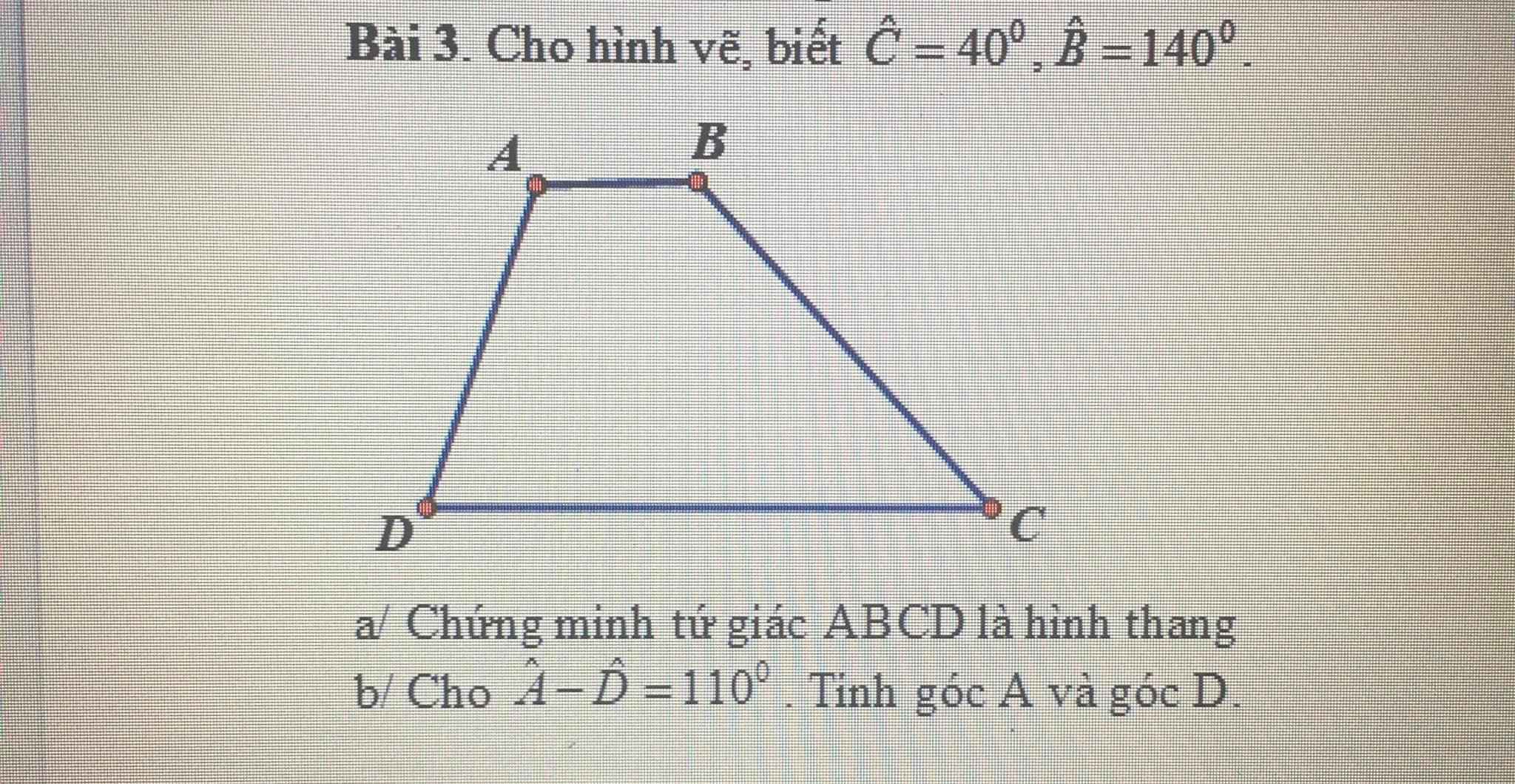

 ai giải giúp mình với ạ mình cảm ơn
ai giải giúp mình với ạ mình cảm ơn





