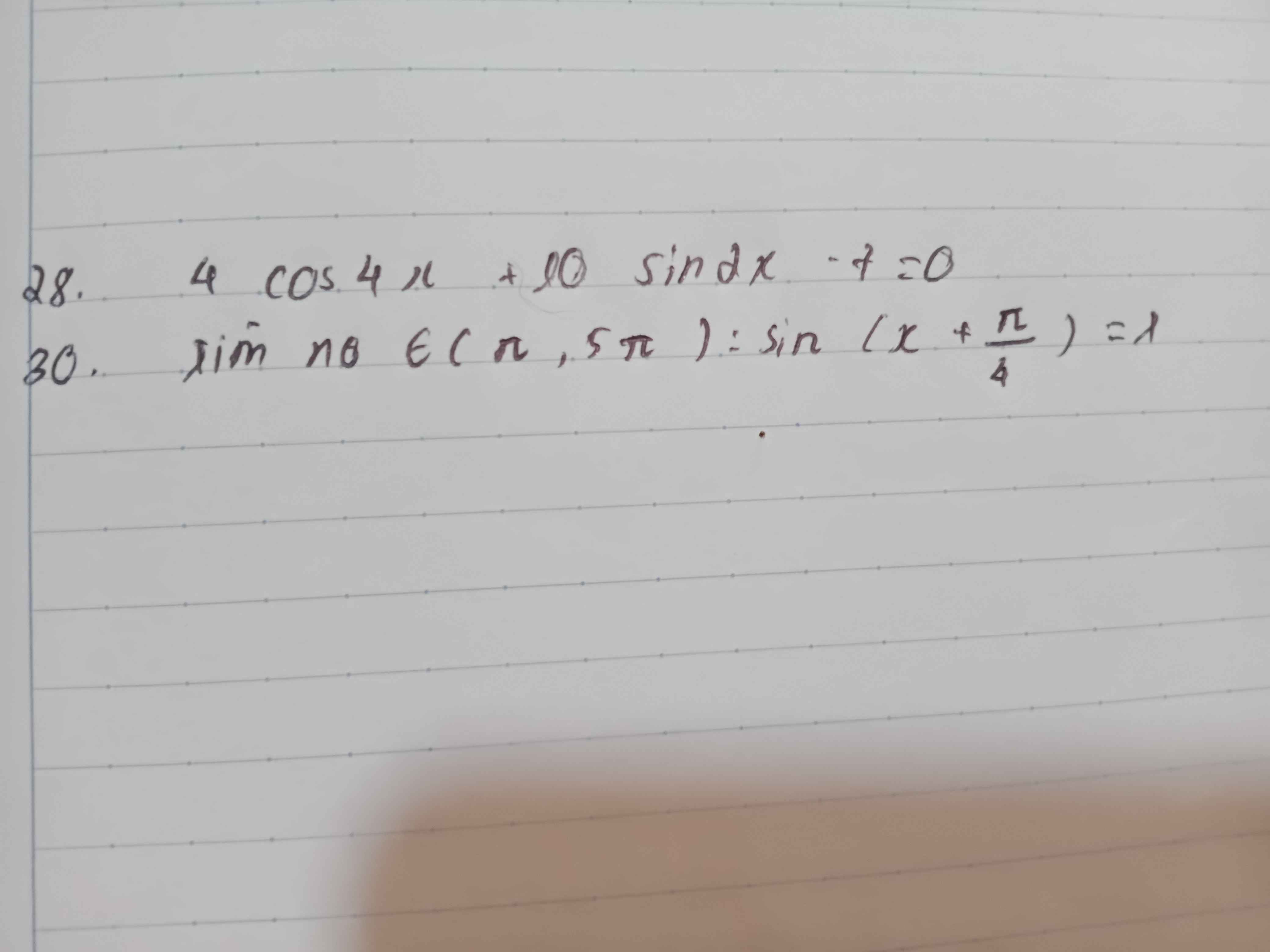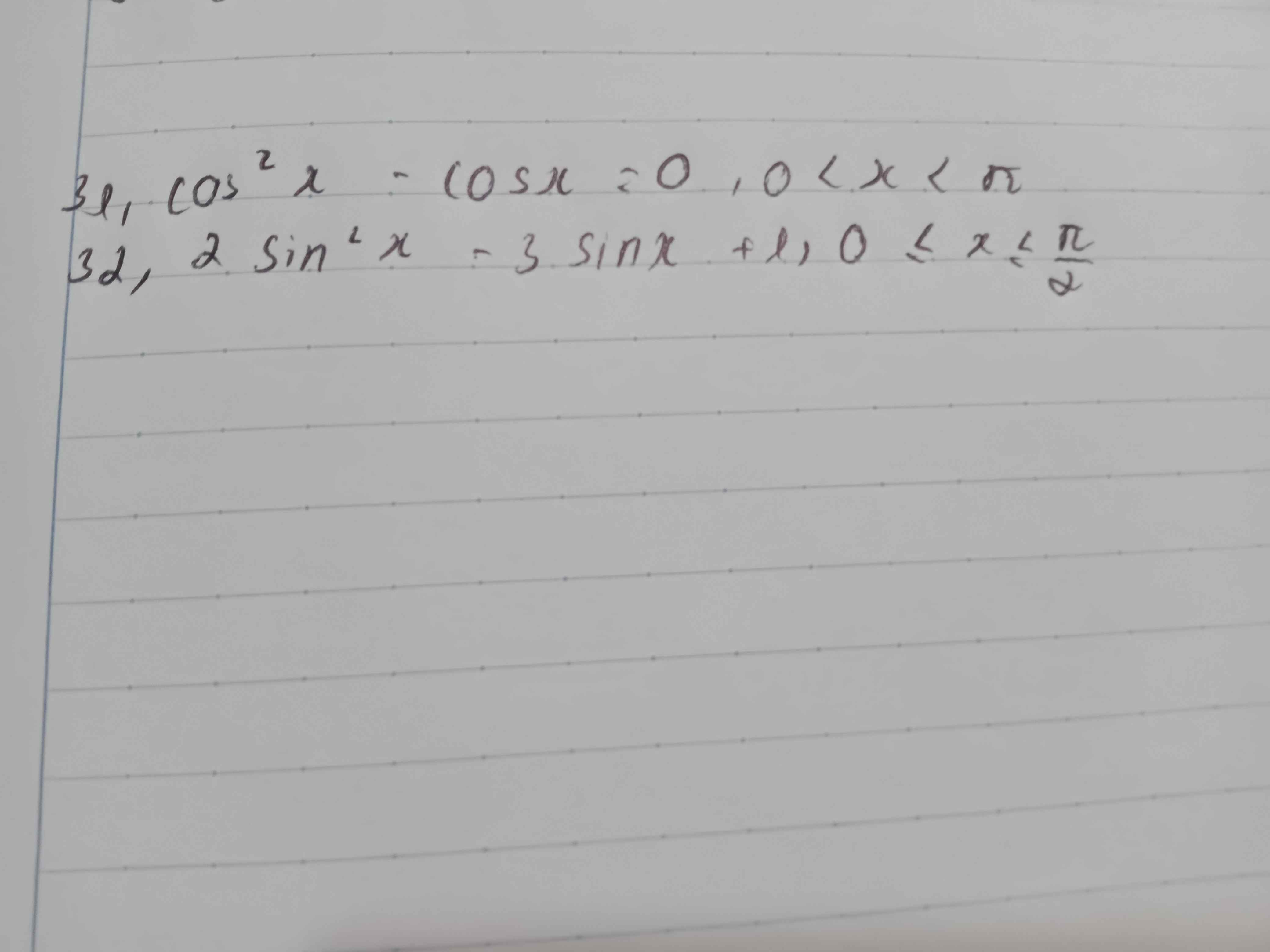28,Pt\(\Leftrightarrow4\left(1-2sin^22x\right)+10sin2x-7=0\)
\(\Leftrightarrow-8sin^22x+10sin2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=\dfrac{3}{4}\\sin2x=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}.arc.sin\left(\dfrac{3}{4}\right)+k\pi\\x=\dfrac{\pi}{2}-arc.sin\left(\dfrac{3}{4}\right)+k\pi\\x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
Vậy..
30,\(sin\left(x+\dfrac{\pi}{4}\right)=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)
\(x\in\left[\pi;5\pi\right]\)\(\Rightarrow\pi\le\dfrac{\pi}{2}+k2\pi\le5\pi\)\(\left(k\in Z\right)\)\(\Leftrightarrow\dfrac{1}{4}\le k\le\dfrac{9}{4}\)\(\left(k\in Z\right)\)
\(\Rightarrow k=\left\{1;2\right\}\)
\(\Rightarrow x=\dfrac{5\pi}{2};x=\dfrac{9\pi}{2}\)