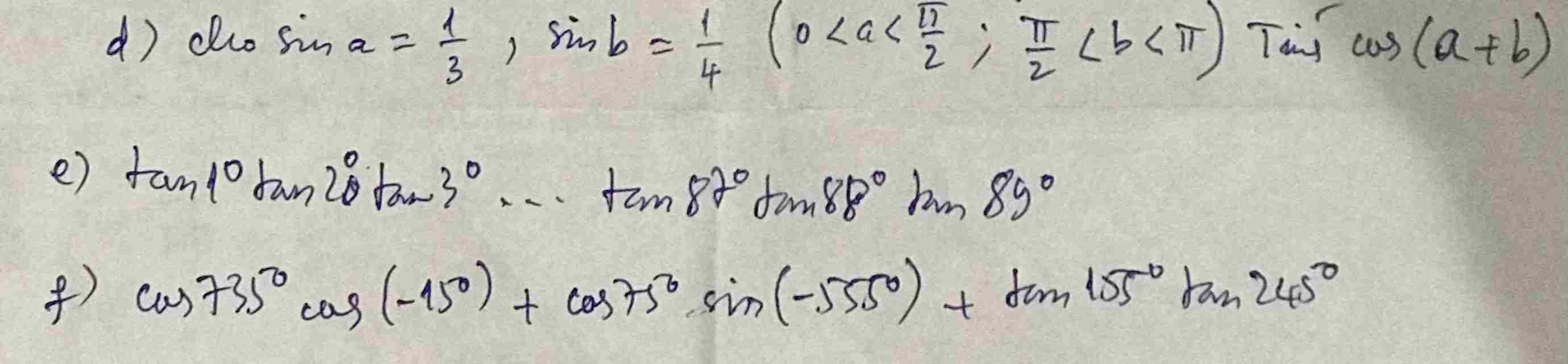d: \(0< a< \dfrac{\Omega}{2}\) nên \(cosa>0\)
\(\dfrac{\Omega}{2}< b< \Omega\) nên cos b<0
\(sin^2a+cos^2a=1\)
=>\(cos^2a=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
mà cos a>0
nên \(cosa=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}\)
\(sin^2b+cos^2b=1\)
=>\(cos^2b=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà cosb<0
nên \(cosb=-\sqrt{\dfrac{15}{16}}=-\dfrac{\sqrt{15}}{4}\)
\(cos\left(a+b\right)=cosa\cdot cosb-sina\cdot sinb\)
\(=\dfrac{2\sqrt{2}}{3}\cdot\dfrac{-\sqrt{15}}{4}-\dfrac{1}{3}\cdot\dfrac{1}{4}=\dfrac{-2\sqrt{30}-1}{12}\)
e: \(tan1^0\cdot tan2^0\cdot...\cdot tan88^0\cdot tan89^0\)
\(=\left(tan1^0\cdot tan89^0\right)\cdot\left(tan2^0\cdot tan88^0\right)\cdot...\cdot\left(tan44^0\cdot tan46^0\right)\cdot tan45^0\)
\(=1\cdot1\cdot...\cdot1=1\)
f: \(cos735^0\cdot cos\left(-15^0\right)+cos75^0\cdot sin\left(-555^0\right)+tan155^0\cdot tan245^0\)
\(=cos735^0\cdot cos15^0+sin15^0\cdot sin735^0+tan155^0\cdot tan245^0\)
\(=cos\left(735-15\right)+\left(-1\right)=1-1=0\)