 giải giúp mik 39 vs ạ , vẽ hình giúp mik lun nhé
giải giúp mik 39 vs ạ , vẽ hình giúp mik lun nhé
Câu 39. Cho \( \triangle ABC \) cân tại \( A \), có \( M \) là trung điểm của \( BC \).
1) Chứng minh: \( AM \) là đường trung trực của \( BC \).
2) Trên tia đối của tia \( MA \) lấy điểm \( N \). Chứng minh: \( \widehat{NBA} = \widehat{NCA} \).
3) Kẻ \( MH \perp AB \) tại \( H \), kẻ \( MK \perp AC \) tại \( K \). Chứng minh:
a) \( \triangle MHB = \triangle MKC \).
b) \( \triangle AHK \) cân.
c) \( HK \parallel BC \).
4) Chứng minh: \( MN \) là đường trung trực của \( HK \).
1: Ta có:AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AM là đường trung trực của BC
2: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔABN và ΔACN có
AB=AC
\(\widehat{BAN}=\widehat{CAN}\)
AN chung
Do đó: ΔABN=ΔACN
=>\(\widehat{ABN}=\widehat{ACN}\)
3:
a: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
\(\widehat{MBH}=\widehat{MCK}\)
Do đó: ΔMHB=ΔMKC
b: ΔMHB=ΔMKC
=>BH=CK
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
=>ΔAHK cân tại A
c: Xét ΔABC có \(\dfrac{AH}{AB}=\dfrac{AK}{AC}\)
nên HK//BC
3: Ta có: MH=MK(ΔMHB=ΔMKC)
=> M nằm trên đường trung trực của HK(1)
Ta có: AH=AK
=>A nằm trên đường trung trực của HK(2)
Từ (1),(2) suy ra AM là đường trung trực của HK
=>NM là đường trung trực của HK











 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
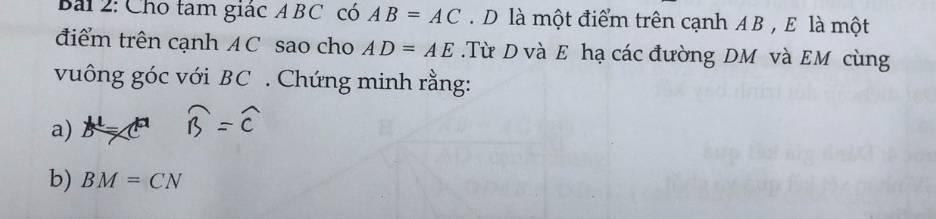





 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ