a: Xét tứ giác AHFC có \(\widehat{AHC}=\widehat{AFC}=90^0\)
nên AHFC là tứ giác nội tiếp
b: Xét tứ giác ABHE có \(\widehat{AEB}=\widehat{AHB}=90^0\)
nên ABHE là tứ giác nội tiếp
=>\(\widehat{AEH}+\widehat{ABH}=180^0\)
mà \(\widehat{AEH}+\widehat{HED}=180^0\)(hai góc kề bù)
nên \(\widehat{HED}=\widehat{ABC}\)
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)
=>\(\widehat{HED}=\widehat{ADC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên HE//CD
a) Ta có:
- ∠HAF = ∠HCF (do cùng chắn cung HF của đường tròn (O))
- ∠AHF = ∠CHF (do cùng chắn cung HC của đường tròn (O))
=> Vậy tứ giác AHFC có 2 cặp góc đối bằng nhau nên tứ giác AHFC nội tiếp.
b) Ta có: ∠HED = ∠HFD = 90^o (do cùng vuông góc với AD)
∠EHD = ∠FHD (do cùng chắn cung HD của đường tròn (O))
- Vậy tam giác HED cân tại H, suy ra HE = HD.
- Tương tự, tam giác HFD cân tại H nên HF = HD. Vậy HE = HF.
- Do đó, tam giác HEF là tam giác cân tại H, suy ra I là trung điểm của EF chính là tâm đường tròn ngoại tiếp tam giác HEF.
- Vì HE = HD và ∠HED = ∠HCD = 90 độ nên tam giác HED đồng dạng với tam giác HCD (cạnh huyền - cạnh góc vuông).
- Từ đó suy ra HE // CD.
=> Vậy ta đã chứng minh được HE // CD và I là tâm đường tròn ngoại tiếp tam giác HEF.





















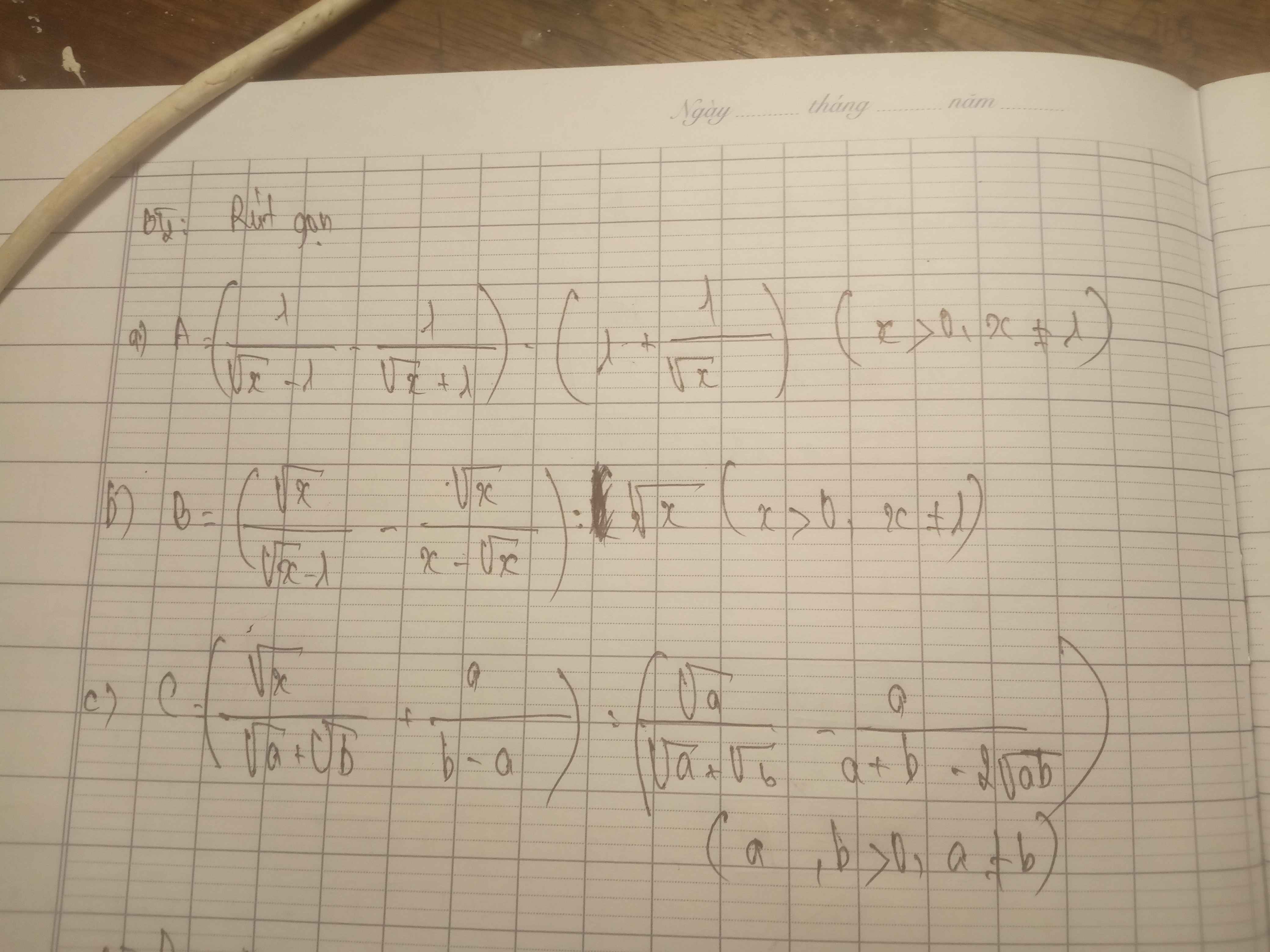

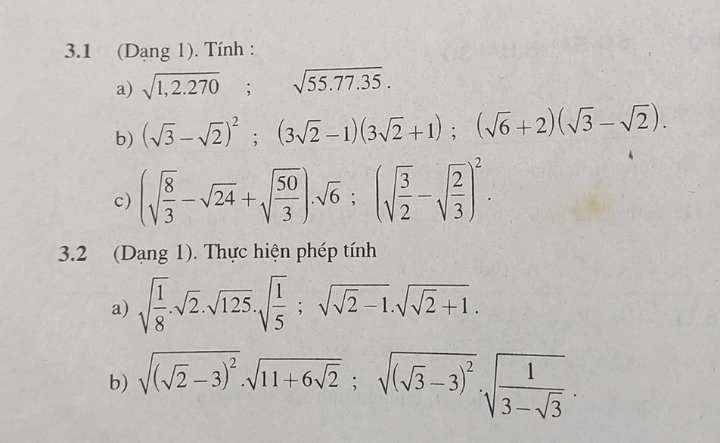
 giúp em giải chi tiết với ạ
giúp em giải chi tiết với ạ