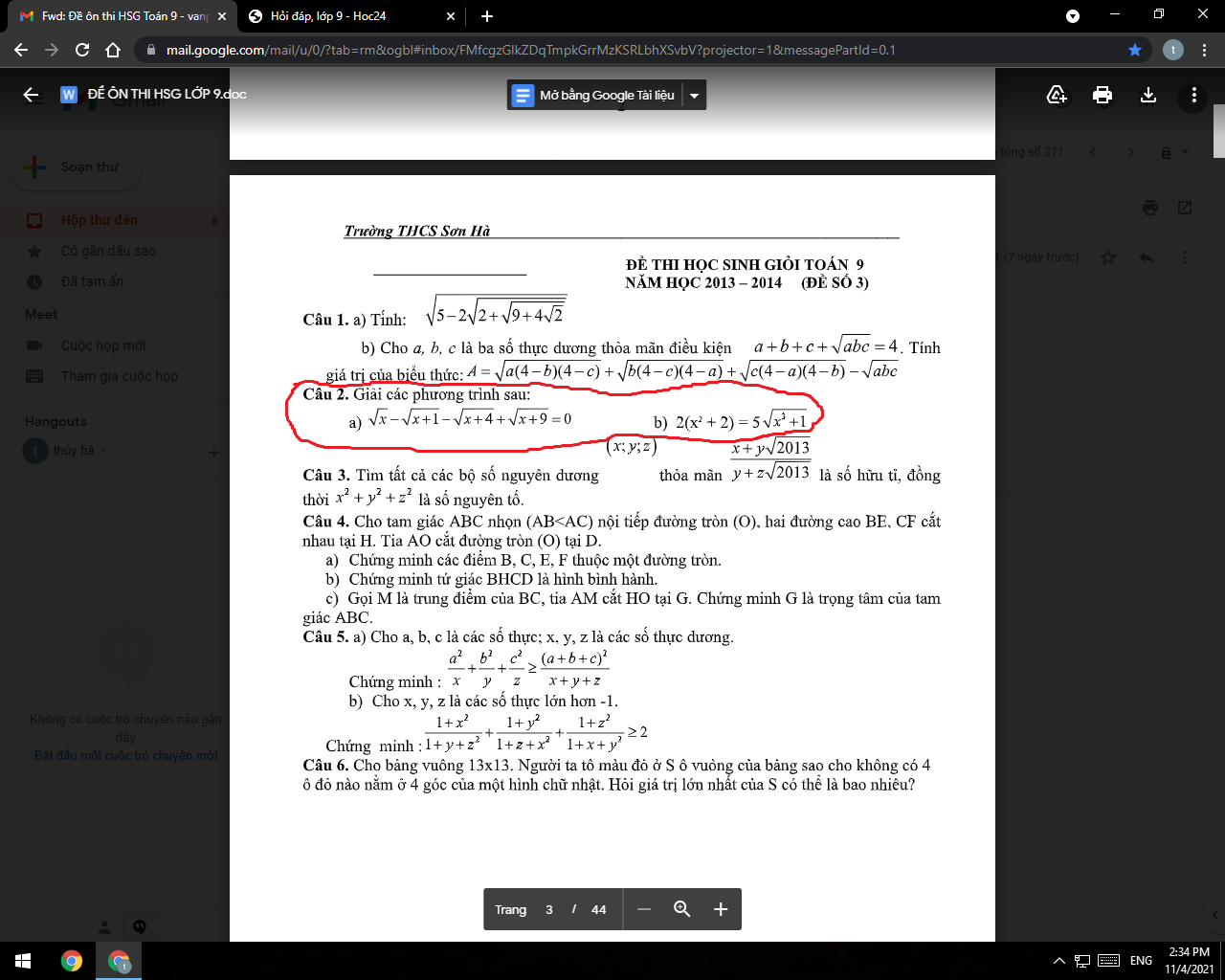
Câu 2:
\(a,ĐK:x\ge0\\ PT\Leftrightarrow\sqrt{x}-\left(\sqrt{x+1}-1\right)-\left(\sqrt{x+4}-2\right)+\left(\sqrt{x+9}-3\right)=0\\ \Leftrightarrow\sqrt{x}-\dfrac{x}{\sqrt{x+1}+1}-\dfrac{x}{\sqrt{x+4}+2}+\dfrac{x}{\sqrt{x+9}+3}=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}-\dfrac{\sqrt{x}}{\sqrt{x+1}+1}-\dfrac{\sqrt{x}}{\sqrt{x+4}+2}+\dfrac{\sqrt{x}}{\sqrt{x+9}+3}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\\sqrt{x}-\dfrac{\sqrt{x}}{\sqrt{x+1}+1}-\dfrac{\sqrt{x}}{\sqrt{x+4}+2}+\dfrac{\sqrt{x}}{\sqrt{x+9}+3}=0\left(1\right)\end{matrix}\right.\)
Với \(x\ge0\Leftrightarrow\left(1\right)>0\)
Vậy PT có nghiệm x=0
\(b,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\), PTTT:
\(2\left(a^2+b^2\right)=5ab\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\\ \forall a=2b\Leftrightarrow x+1=4\left(x^2-x+1\right)\\ \Leftrightarrow4x^2-5x+3=0\\ \Delta=25-48< 0\\ \Leftrightarrow x\in\varnothing\\ \forall b=2a\Leftrightarrow x^2-x+1=4\left(x+1\right)\\ \Leftrightarrow x^2-5x-3=0\\ \Delta=25+12=37\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(n\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(n\right)\end{matrix}\right.\)
Vậy ...