`1)x^3/(x+1975)*(2x+1954)/(x+1)+x^3/(x+1975)*(21-x)/(x+1)`
`=(x^3(2x+1954))/((x+1975)(x+1))+(x^3(21-x))/((x+1975)(x+1))`
`=(2x^4+1954x^3+21x^3-x^4)/((x+1975)(x+1))`
`=(x^4+1975x^3)/((x+1975)(x+1))`
`=(x^3(x+1975))/((x+1975)(x+1))`
`=x^3/(x+1)`
`2)(19x+8)/(x-7)*(5x-9)/(x+1945)-(19+8)(x-7)*(4x-2)/(x+1945)`
`=(19x+8)/(x-7)*((5x-9)/(x+1945)-(4x-2)/(x+1945))`
`=(19x+8)/(x-7)*((5x-9-4x+2)/(x+1945))`
`=(19x+8)/(x-7)*(x-7)/(x+1945)`
`=(19x+8)/(x+1945)`
3: \(\dfrac{x^3-1}{x+2}\left(\dfrac{1}{x-1}-\dfrac{x+1}{x^2+x+1}\right)\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x+2}\cdot\dfrac{x^2+x+1-\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1-x^2+1}{x+2}=\dfrac{x+2}{x+2}=1\)
4: \(\dfrac{x^3+2x^2-x-2}{2x+10}\left(\dfrac{1}{x-1}-\dfrac{2}{x+1}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{x^2\left(x+2\right)-\left(x+2\right)}{2\left(x+5\right)}\cdot\left(\dfrac{1}{x-1}-\dfrac{2}{x+1}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x^2-1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{x+1-2x+2}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{-x+3}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\dfrac{\left(-x+3\right)\left(x+2\right)+x^2-1}{\left(x+2\right)\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{-x^2-2x+3x+6+x^2-1}{2\left(x+5\right)}=\dfrac{x+5}{2\left(x+5\right)}=\dfrac{1}{2}\)
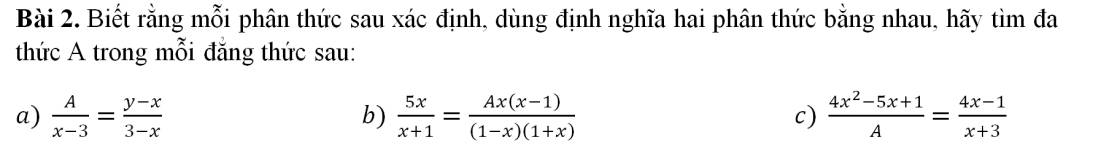giúp em bài này với ạ ! Em cảm ơn ạ 
cd
