Vì 2<>1 nên (d) luôn cắt (d')
Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}2x+2m^2+m+3=x+m^2+3\\y=x+m^2+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=m^2+3-2m^2-m-3\\y=x+m^2+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-m^2-m\\y=-m^2-m+m^2+3=-m+3\end{matrix}\right.\)
Để x+y>0 thì \(-m^2-m+\left(-m\right)+3>0\)
=>\(-m^2-2m+3>0\)
=>\(m^2+2m-3< 0\)
=>(m+3)(m-1)<0
=>-3<m<1










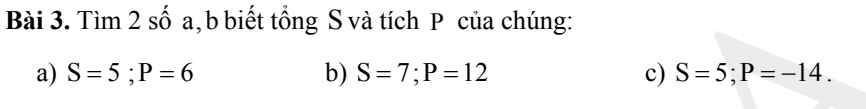
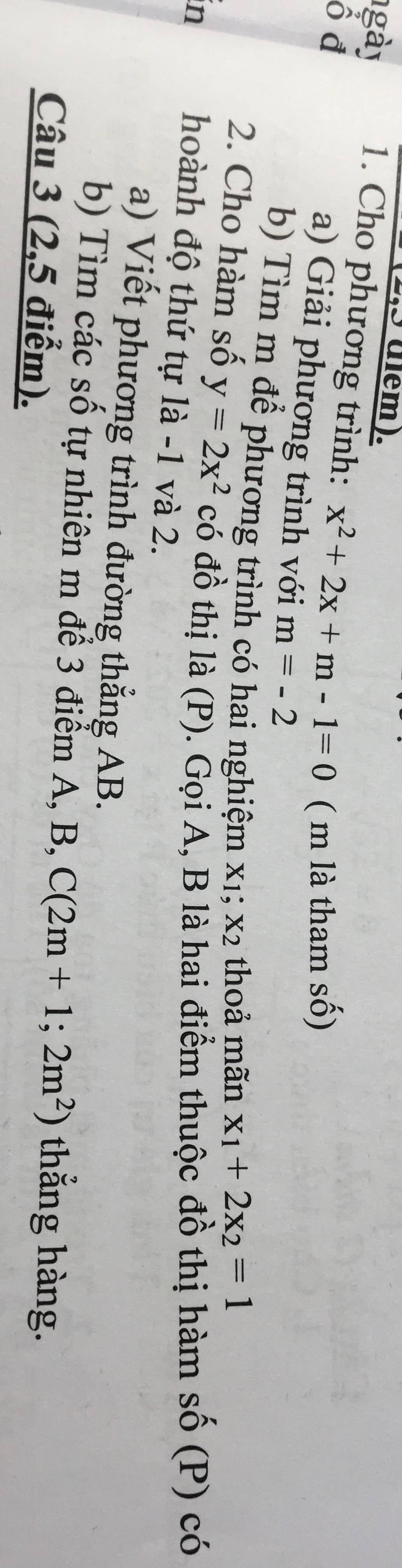
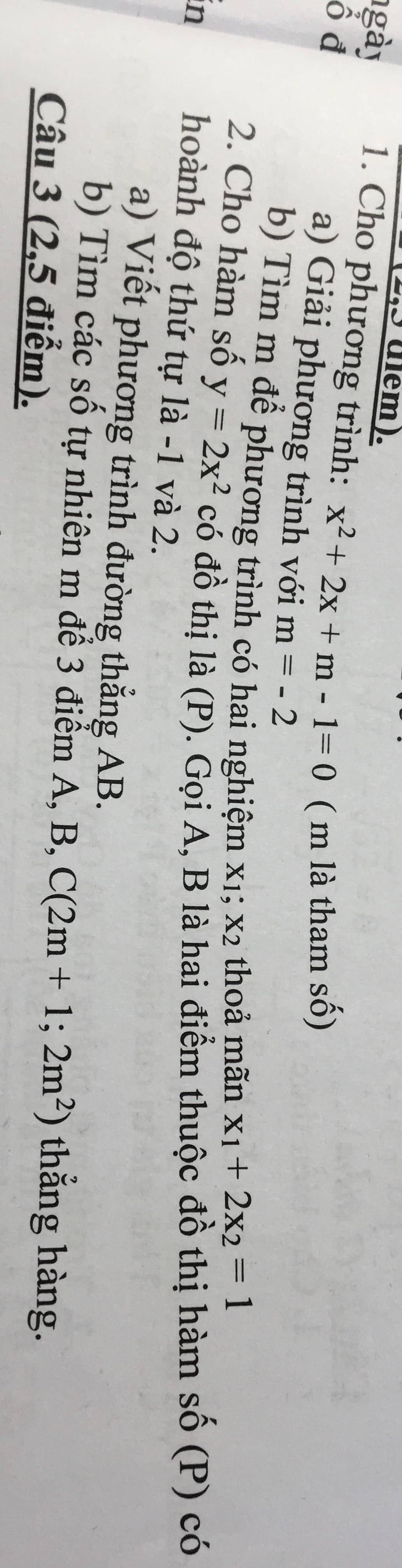




 Giúp em giải bài tập này với ạ. Em cảm ơn.
Giúp em giải bài tập này với ạ. Em cảm ơn.


