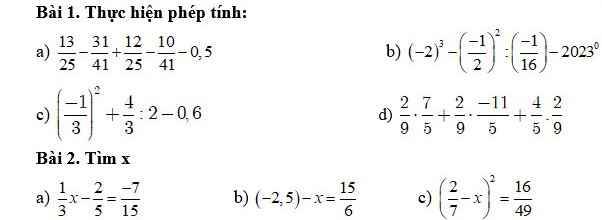a.
Xét hai tam giác BAH và CAH có:
\(\left\{{}\begin{matrix}AB=AC\left(\Delta ABC\text{ cân tại A}\right)\\\widehat{BAH}=\widehat{CAH}\left(\text{AH là phân giác}\right)\\AH\text{ là cạnh chung}\end{matrix}\right.\)
\(\Rightarrow\Delta BAH=\Delta CAH\left(c.g.c\right)\)
\(\Rightarrow BH=CH\)
\(\Rightarrow H\) là trung điểm của BC
b.
Xét hai tam giác vuông AKH và AMH có:
\(\left\{{}\begin{matrix}\text{AH là cạnh chung}\\\widehat{KAH}=\widehat{MAH}\left(\text{AH là phân giác}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}AKH=\Delta_{\perp}AMH\left(ch-gn\right)\) (1)
\(\Rightarrow AK=AM\) (2)
\(\Rightarrow\Delta AKM\) cân tại A
c.
Cũng từ (1) \(\Rightarrow HK=HM\) (3)
Từ (2);(3) \(\Rightarrow AH\) là trung trực của KM
\(\Rightarrow AH\perp KM\)

 Giải gấp giúp mình ạ
Giải gấp giúp mình ạ


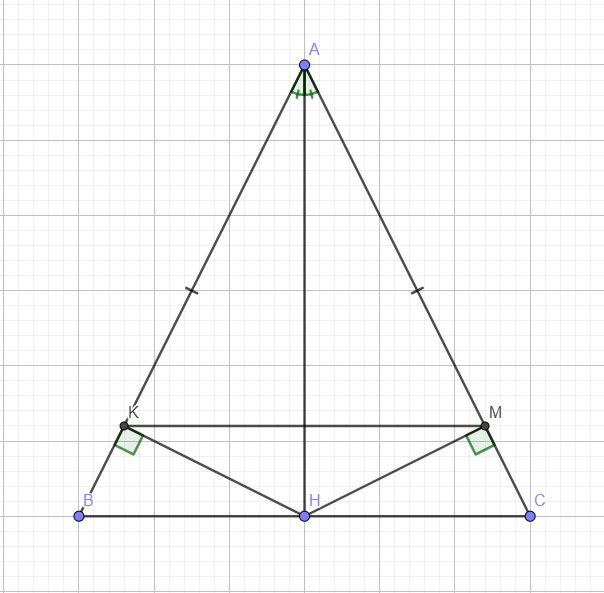

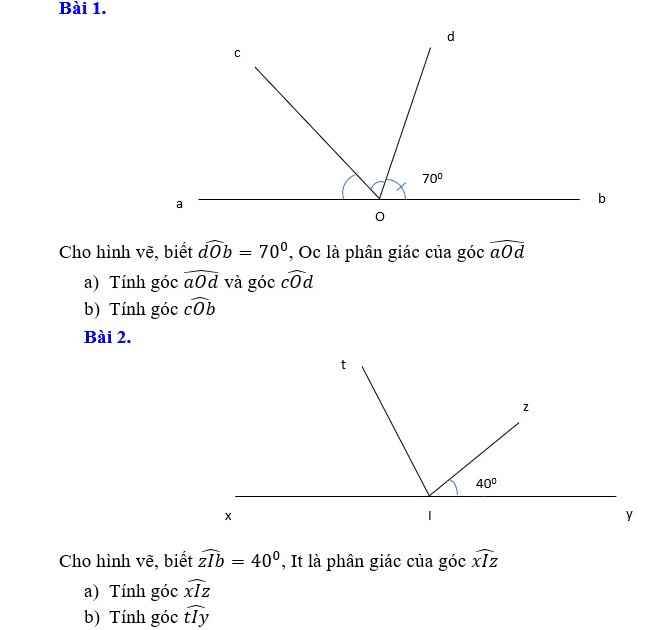
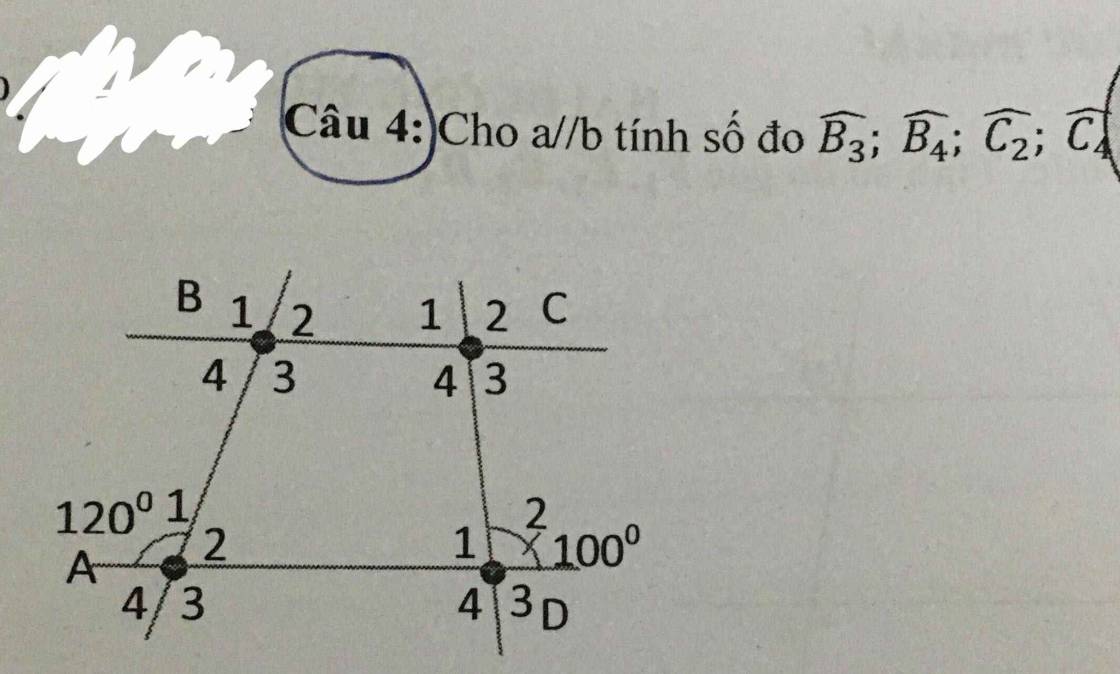
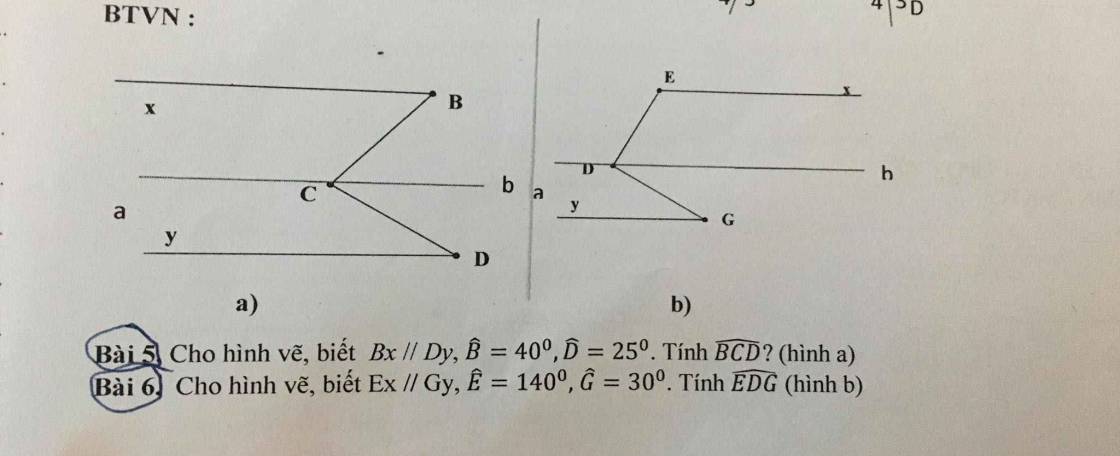
 Mg giải giúp mình ạ mình đang rất gấp
Mg giải giúp mình ạ mình đang rất gấp Mg giải gấp giúp mình ạ
Mg giải gấp giúp mình ạ Mg giải gấp giúp mình ạ
Mg giải gấp giúp mình ạ