Question

Giải chi tiết giúp mình với ạ

Answer 1

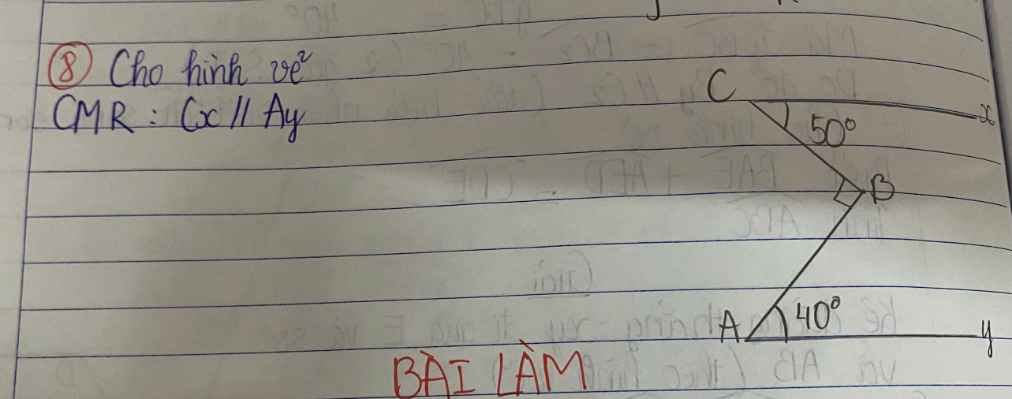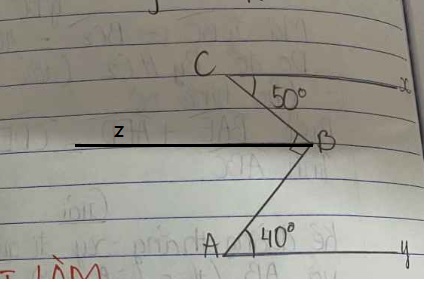
Qua B vẽ tia \(Bz||Cx\) (1)

Do \(Bz||Cx\) nên \(\widehat{CBz}=\widehat{BCx}\) (hai góc so le trong)

Suy ra \(\widehat{CBz}=50^0\)

Mà \(\widehat{CBz}+\widehat{ABz}=\widehat{CBA}\)

\(50^0+\widehat{ABz}=90^0\)

\(\widehat{ABz}=90^0-50^0=40^0\)

Suy ra \(\widehat{ABz}=\widehat{BAy}\)

Mà \(\widehat{ABz}\) và \(\widehat{BAy}\) là hai góc so le trong

Suy ra \(Bz||Ay\) (2)

Từ (1);(2) suy ra \(Cx||Ay\)