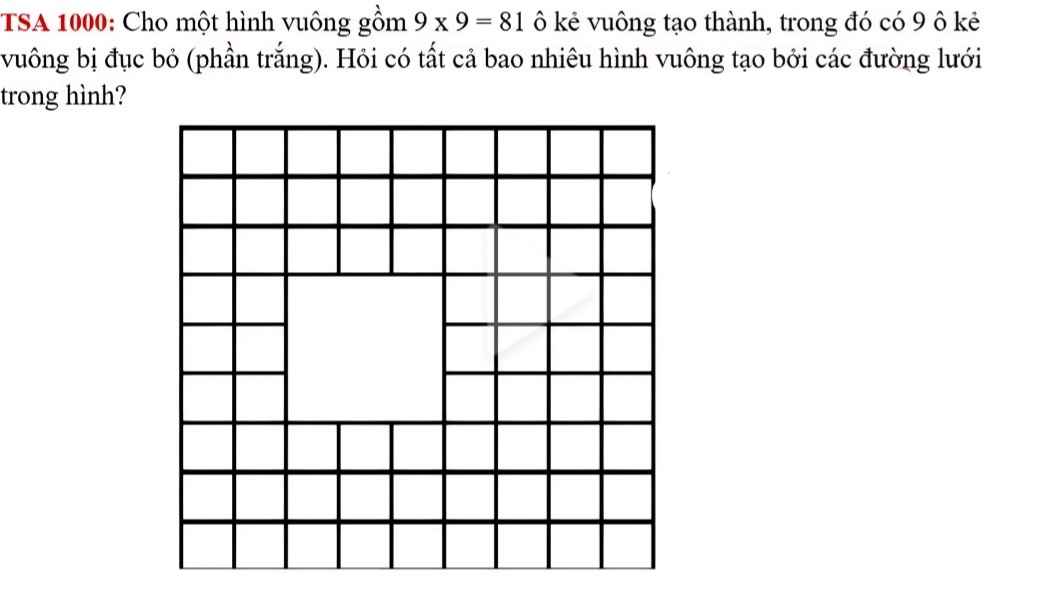
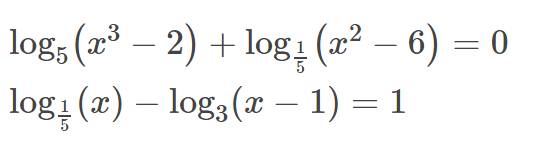Gọi A1 là tập hợp các hình vuông nằm trong hình chữ nhật 9x3 (ở phía trên) ; A2 là tập hợp các hình vuông nằm trong hình chữ nhật 2x9 ; A3 là tập hợp các hình vuông nằm trong hình chữ nhật 9x3 (ở phía dưới) , và A4 là tập hợp các hình vuông nằm trong hình chữ nhật 4x9. Dễ thấy \(\left|A_1\right|=\left|A_3\right|\).
Số các hình vuông nằm trong hình chữ nhật 9x3 ở phía trên (phía dưới) là: \(\left|A_1\right|=\left|A_3\right|=9.3+8.2+7.1=50\) (hình vuông).
Số các hình vuông nằm trong hình chữ nhật 2x9 là: \(\left|A_2\right|=2.9+1.8=26\) (hình vuông).
Số các hình vuông nằm trong hình chữ nhật 4x9 là: \(\left|A_4\right|=4.9+3.8+2.7+1.6=80\) (hình vuông).
Số các hình vuông vừa nằm trong hình chữ nhật 9x3 ở phía trên, vừa nằm trong hình chữ nhật 2x9 là: \(\left|A_1\cap A_2\right|=2.3+1.2=8\) (hình vuông)
Tương tự, ta có: \(\left|A_2\cap A_3\right|=2.3+1.2=8\) (hình vuông) ; \(\left|A_3\cap A_4\right|=4.3+3.2+2.1=20\) (hình vuông), \(\left|A_4\cap A_1\right|=4.3+3.2+2.1=20\) (hình vuông).
Dễ thấy \(\left|A_1\cap A_3\right|=\left|A_1\cap A_4\right|=\left|A_2\cap A_4\right|=0\), và \(\left|A_i\cap A_j\cap A_k\right|=\left|A_1\cap A_2\cap A_3\cap A_4\right|=0,\forall1\le i< j< k\le4\).
Theo nguyên lí bao hàm và loại trừ, ta có:
\(\left|A_1\cup A_2\cup A_3\cup A_4\right|=\sum\limits^4_{i=1}\left|A_i\right|-\sum\limits\left|A_i\cap A_j\right|^{ }_{1\le i< j\le4}+\sum\limits\left|A_i\cap A_j\cap A_k\right|^{ }_{1\le i< j< k\le4}-\left|A_1\cap A_2\cap A_3\cap A_4\right|=50+50+26+80-8-8-20-20=150\)(hình vuông)
Đáp án: 150 hình vuông.