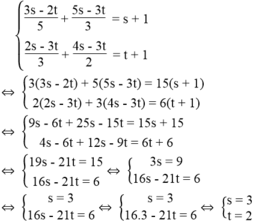
Vậy hệ phương trình đã cho có nghiệm (s; t) = (3;2)
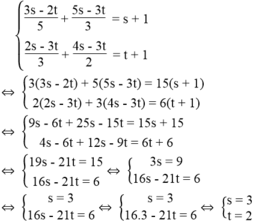
Vậy hệ phương trình đã cho có nghiệm (s; t) = (3;2)
giải các hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{2x+1}{4}-\dfrac{y-2}{3}=\dfrac{1}{12}\\\dfrac{x+5}{2}=\dfrac{y+7}{3}-4\end{matrix}\right.\)
b2.
\(A=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)
B3. Tìm ĐKXĐ
\(\dfrac{1}{x\sqrt{x}+1}-\dfrac{2}{\sqrt{x}+1}\)
b4. so sánh A với 1
A=\(\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\)
b5.tính
a,\(\sin47+2\sin38-\cos43-\cos52\)
b, \(C=\dfrac{2\sin^2x-1}{\sin x-\cos x}\)
Tính các giá trị tương ứng của s khi cho t lần lượt lấy các giá trị 1 giờ; 2 giờ; 3 giờ; 4 giờ; … rồi giải thích tại sao s là hàm số của t ?
Tính các giá trị tương ứng của s khi cho t lần lượt lấy các giá trị 1 giờ; 2 giờ; 3 giờ; 4 giờ; … rồi giải thích tại sao s là hàm số của t ?
Giải các hệ phương trình theo hai cách:
*Cách thứ nhất: đưa hệ phương trình về dạng: a x + b y = c a ' x + b ' y = c '
*Cách thứ hai: đặt ẩn phụ, chẳng hạn s = 3x – 2, t = 3y + 2
2 3 x - 2 - 4 = 5 3 y + 2 4 3 x - 2 + 7 3 y + 2 = - 2
bài 1 : Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình :
a) 5 + 2x – 4 = 0 ;
b) 4 – 6
x + 4 = 0 ;
bài 2 :
Dùng hệ thức Vi-ét để tính nhẩm nghiệm của phương trình :
a) 7 + 3x – 4 = 0 ;
b) 4 – (5 +
) x + 1 +
= 0.
Tính tích S tất cả các nghiệm nguyên khác 0 của phương trình |x-2|+|x+3|=5
phưcho phương trình x2 - 2 ( 2m + 1 )x + 3 + 4m = 0 (1)
a > Tìm hệ thức giữa x1 S x2 độc lập với m .
b > Tính m biểu thức A = X13 + X23.
c > Tìm m để (1) có 1 nghiệm gấp 3 lần nghiệm kia .
d > Lập phương trình bậc hai có các nghiệm là X12 , X22
Tính giá trị của biểu thức:
a) S = 1/(1*3*5) + 1/(3*5*7) + ... + 1/(2011*2013*2015)
b) Tính T= (2tanx-3cotx)/(4tanx+5cotx) + 6sinx^2 - 7cos^3x biết cosx= 3/4
Giải các hệ phương trình theo hai cách:
*Cách thứ nhất: đưa hệ phương trình về dạng: a x + b y = c a ' x + b ' y = c '
*Cách thứ hai: đặt ẩn phụ, chẳng hạn s = 3x – 2, t = 3y + 2
3 x + y - 5 x - y = 12 - 5 x + y + 2 x - y = 11