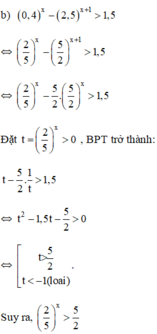
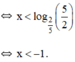
Vậy bất phương trình có tập nghiệm (-∞; -1)
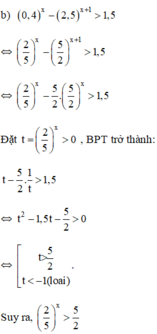
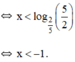
Vậy bất phương trình có tập nghiệm (-∞; -1)
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Giải các bất phương trình sau: (x − 5)(logx + 1) < 0
1.Giải phương trình:
3x^4+x^2-4=03\(x^4\) +\(x^2\) - 4=0
\dfrac{4}{5}
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Giải các bất phương trình sau: (2x − 7)ln(x + 1) > 0
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Giải bất phương trình sau log 1 5 ( 3 x - 5 ) > log 1 5 ( x + 1 )
![]()
![]()
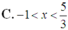
![]()
Giải các phương trình sau trên tập số phức:
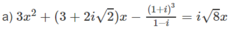
b) ( 1 - i x ) 2 + (3 + 2i)x − 5 = 0
Giải bất phương trình 2 x + 5 - 5 - x ≥ 3 x - 2 ( x ∈ R )
![]()
![]()
![]()
![]()
Câu 1: Tìm GTLN và GTNN của hàm số: y= ex + 2x -3ln(x + 1) , \(x\in[1;3]\)
Câu 2: Giải phương trình và bất phương trình sau:
a) \(log_{\sqrt{3}}(x-4)=1+log_3\left(x-2\right)\)
b) \(4^x-3.2^{x+1}+5\ge0\)