a: Xét ΔACN vuông tại C có CB là đường cao
nên \(AB\cdot AN=AC^2\left(1\right)\)
Xét ΔACM vuông tại C có CD là đường cao
nên \(AD\cdot AM=AC^2\left(2\right)\)
Từ (1),(2) suy ra \(AB\cdot AN=AD\cdot AM\)
b: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC^2=3^2+4^2=9+16=25=5^2\)
=>AC=5(cm)
Ta có: \(AD\cdot AM=AC^2\)
=>\(AM\cdot3=5^2\)
=>\(AM=\frac{5^2}{3}=\frac{25}{3}\left(\operatorname{cm}\right)\)
Ta có: AD+DM=AM
=>\(DM=AM-AD=\frac{25}{3}-3=\frac{25}{3}-\frac93=\frac{16}{3}\) (cm)
ΔACM vuông tại C
=>\(AC^2+CM^2=AM^2\)
=>\(CM^2=\left(\frac{25}{3}\right)^2-5^2=\frac{625}{9}-25=\frac{400}{9}\)
=>\(CM=\sqrt{\frac{400}{9}}=\frac{20}{3}\) (cm)
Xét ΔACM vuông tại C có \(tanAMC=\frac{AC}{CM}\)
=>tan AMN\(=5:\frac{20}{3}=5\cdot\frac{3}{20}=\frac{15}{20}=\frac34\)
c:
Xét ΔAMN vuông tại A có AC là đường cao
nên \(AM\cdot AN=AC\cdot MN\)
\(AB\cdot AN=AC^2\)
=>\(AN=\frac{AC^2}{AB}\)
\(AD\cdot AM=AC^2\)
=>\(AD=\frac{AC^2}{AM}\)
\(CD\cdot CB=AD\cdot AB=\frac{AC^2}{AN}\cdot\frac{AC^2}{AM}\)
\(=\frac{AC^4}{AN\cdot AM}=\frac{AC^4}{AC\cdot MN}=\frac{AC^3}{MN}\)

 giải c) d) cho mình vs
giải c) d) cho mình vs












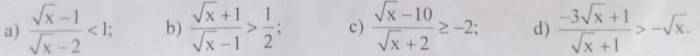 giải câu c và d hộ mik vs
giải câu c và d hộ mik vs