Chọn B.
TXĐ: D = R. Nhận xét: Hàm số f(x) liên tục trên R
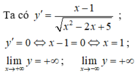
Bảng biến thiên
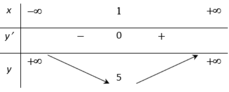
Do đó m i n ℝ y = 5
Chọn B.
TXĐ: D = R. Nhận xét: Hàm số f(x) liên tục trên R
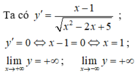
Bảng biến thiên

Do đó m i n ℝ y = 5
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Cho hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 . Tập giá trị của m để y ' ≥ 0 ∀ x ∈ ℝ là
A. [3;+ ∞ )
B. ∅
C. [ 4 2 ;+ ∞ )
D. [1;+ ∞ )
Cho a , b ∈ ℝ , 0 < a < b, hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f'(x) < 0, ∀ x ∈ ( a ; b ) . Giá trị nhỏ nhất của hàm số đã cho trên đoạn [a;b] bằng
A. f(b)
B. f a + b 2
C. f(a)
D. f a b
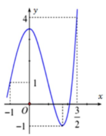
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên - 1 ; 3 2 . Giá trị của M - N bằng
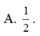
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + 2 ( m - 1 ) x 2 + ( m - 1 ) x + 5 đồng biến trên ℝ
A. m ∈ ( - ∞ ; 1 ]
B. m ∈ 1 ; 7 4
C. m ∈ - ∞ ; 1 ∪ 7 4 ; + ∞
D. m ∈ 1 ; 7 4
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ -1
D. m ≤ -1
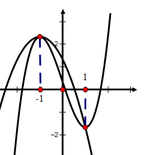
Cho hàm số y = x 3 + ax 2 + bx + c ( a , b , c ∈ ℝ ) có đồ thị (C) và y = mx 2 + nx + p ( m , n , p ∈ ℝ ) có đồ thị (P) như hình vẽ. Tính diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?
A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
Có bao nhiêu giá trị nguyên nhỏ hơn 2019 của m để hàm số y = x 3 - m x + 1 có 5 điểm cực trị trên ℝ ?
![]()
![]()
![]()
![]()
Cho m, n không đồng thời bằng 0. Tìm điều kiện của m, n để hàm số y = msin x - ncos x - 3 x nghịch biến trên ℝ .
![]()
![]()
![]()
![]()
Với gia trị nào của tham số m thì hàm số y = - 1 3 x 3 - m x 2 + ( 2 m - 3 ) x - m + 2 nghịch biến trên ℝ ?
A. -3 ≤ m ≤ 1
B. m ≤ 1
A. m ≤ -3 hoặc m ≥ 1
D. -3 < m < 1