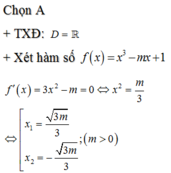Các câu hỏi tương tự
Cho hàm số
y
f
x
xác định trên
ℝ
và có bảng biến thiên như hình vẽ: Hỏi có bao nhiêu giá trị của tham số m (với
m
∈
ℤ
;
m
≤
2019
) để đồ thị hàm số
y
m
+
f
x
có đúng 7 điểm cực trị?
Đọc tiếp
Cho hàm số y = f x xác định trên ℝ và có bảng biến thiên như hình vẽ:
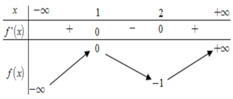
Hỏi có bao nhiêu giá trị của tham số m (với m ∈ ℤ ; m ≤ 2019 ) để đồ thị hàm số y = m + f x có đúng 7 điểm cực trị?
![]()
![]()
![]()
![]()
Cho hàm số y f ( x) có đạo hàm
f
x
x
+
1
4
x
-
m
5
x...
Đọc tiếp
Cho hàm số y = f ( x) có đạo hàm f ' x = x + 1 4 x - m 5 x + 3 3 với mọi x ∈ ℝ . Có bao nhiều giá trị nguyên của tham số m ∈ - 5 ; 5 để hàm số g x = f x có 3 điểm cực trị?
A. 3.
B. 6.
C. 5.
D. 4.
Cho hàm số y
(
m
-
1
)
x
3
-
5
x
2
+
(
m
+
3
)
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của m để hàm số yf(|x|) có đúng 3 điểm cực trị? A. 5. B. 3. C. 4. D. 0.
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 5 x 2 + ( m + 3 ) x + 3 . Có tất cả bao nhiêu giá trị nguyên của m để hàm số y=f(|x|) có đúng 3 điểm cực trị?
A. 5.
B. 3.
C. 4.
D. 0.
Cho hàm số
y
(
m
-
1
)
x
3
-
5
x
2
+
(
m
+
3
)
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của m để hàm số
y
f
x
có đúng 3 điểm cực trị? A. 5 B. 3 C. 4 D. 0
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 5 x 2 + ( m + 3 ) x + 3 . Có tất cả bao nhiêu giá trị nguyên của m để hàm số y = f x có đúng 3 điểm cực trị?
A. 5
B. 3
C. 4
D. 0
Cho hàm số f(x) xác định và liên tục trên
ℝ
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình
2
f
3
-
3
-
9
x
2
+
30
x
-...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên ℝ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình 2 f 3 - 3 - 9 x 2 + 30 x - 21 = m - 2019 có nghiệm.
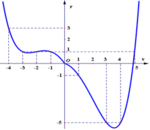
A. 15
B. 14
C. 10
D. 13
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
+
m
x
2
+
2
đồng biến trên
ℝ
? A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + m x 2 + 2 đồng biến trên ℝ ?
A. 1
B. 2
C. 4
D. 3
Tìm tất cả các giá trị của tham số m để hàm số y
x
+
m
x
2
+
x
+
1
có giá trị lớn nhất trên
ℝ
nhỏ hơn hoặc bằng 1. A. m
≤
1 B. m
≥
1 C. m
≥
-1 D. m
≤
-1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ -1
D. m ≤ -1
Cho hàm số
f
(
x
)
x
3
-
(
m
-
1
)
x
2
+
(
5
-
m
)
x
+
m
2
-
5
. Có bao nhiêu giá trị nguyên của tham số m để hàm số
g
x
f
x
có 5 đi...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - ( m - 1 ) x 2 + ( 5 - m ) x + m 2 - 5 . Có bao nhiêu giá trị nguyên của tham số m để hàm số g x = f x có 5 điểm cực trị?
A. 0.
B. 1.
C. 2.
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để điểm M(2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số
y
2
x
3
-
3
(
2
m
+
1
)
x
2
+
6
m
(
m
+
1
)
x
+
1
(C) một tam giác có...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để điểm M(2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 (C) một tam giác có diện tích nhỏ nhất
A. 0
B. 1
C. 2
D. Không tồn tại