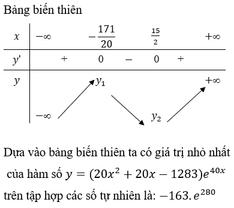
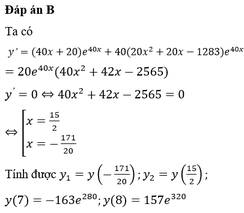Các câu hỏi tương tự
Giá trị nhỏ nhất, lớn nhất của hàm số
y
x
−
ln
x
trên đoạn
1
2
;
e
theo thứ tự là A. 1 và
e
−
1
. B.
1
2
+
ln
2
và
e
−
1
. C. 1 và
e
....
Đọc tiếp
Giá trị nhỏ nhất, lớn nhất của hàm số y = x − ln x trên đoạn 1 2 ; e theo thứ tự là
A. 1 và e − 1 .
B. 1 2 + ln 2 và e − 1 .
C. 1 và e .
D. 1 và 1 2 + ln 2 .
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y x ln(x) trên đoạn
1
2
;
e
lần lượt là A. 1 và e - 1 B. 1 và e C.
1
2
+
ln
2
và e - 1 D. 1 và
1
2
+
ln
2
Đọc tiếp
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x = ln(x) trên đoạn 1 2 ; e lần lượt là
A. 1 và e - 1
B. 1 và e
C. 1 2 + ln 2 và e - 1
D. 1 và 1 2 + ln 2
Giá trị nhỏ nhất của hàm số
y
x
−
3
ln
x
trên đoạn
1
;
e
bằng A. 1. B.
3
−
3
ln
3.
C. e. D.
e
−
3.
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = x − 3 ln x trên đoạn 1 ; e bằng
A. 1.
B. 3 − 3 ln 3.
C. e.
D. e − 3.
Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
.
e
−
x
trên đoạn
−
1
;
1
. Tính tổng M+N. A.
M
+
N
3
e
B.
M
+...
Đọc tiếp
Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 . e − x trên đoạn − 1 ; 1 . Tính tổng M+N.
A. M + N = 3 e
B. M + N = e
C. M + N = 2 e − 1
D. M + N = 2 e + 1
Giả sử đường thẳng yx+m cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y=x+m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81
Giả sử đường thẳng
y
x
+
m
cắt đồ thị (C) của hàm số
y
x
−
1
1
−
2
x
tại hai điểm phân biệt E và F. Gọi
k
1
,
k
2
lần lượt là hệ số góc của các tiếp tuyến với
C
tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức
S...
Đọc tiếp
Giả sử đường thẳng y = x + m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với C tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81
Tìm giá trị nhỏ nhất của hàm số y = e x - e - x - 2 ln ( x + 1 + x 2 ) với x ≥ 0
A. 0
B. 10
C. 2
D. -10
Xác định giá trị a, b, c để hàm số
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của
f
(
x
)
(
x
2
-
3
x
+
2
)
e...
Đọc tiếp
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
tim giá trị nhỏ nhất của biểu thức với X thuộ tập hợp Z
a) D= 2+ giá trị tuyệt đối của X
b) E= giái trị tuyệt đối cua3 - X =2