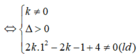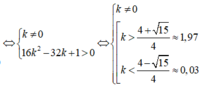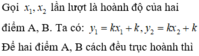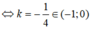Các câu hỏi tương tự
Biết đường thẳng y (3m-1) x+ 6m+3 cắt đồ thị hàm số y x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây? A. (1; 3/2) B. (0;1) C. (-1; 0) D. (3/2; 2)
Đọc tiếp
Biết đường thẳng y= (3m-1) x+ 6m+3 cắt đồ thị hàm số y= x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A. (1; 3/2)
B. (0;1)
C. (-1; 0)
D. (3/2; 2)
Đường thẳng d:yx-3 cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng
△
:
x
-
y
0
Tính dd1+d A. B. C. d 6 D.
Đọc tiếp
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Cho (C) là đồ thị của hàm số
y
x
-
2
x
+
1
Đường thẳng d:yx+m cắt đồ thị (C) tại hai điểm A, B phân biệt và
A
B
2
2
khi m nhận giá trị nào trong các giá trị nào sau đây? A. m 1 B. m 5 C. m -2 D. m 8
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 Đường thẳng d:y=x+m cắt đồ thị (C) tại hai điểm A, B phân biệt và A B = 2 2 khi m nhận giá trị nào trong các giá trị nào sau đây?
A. m = 1
B. m = 5
C. m = -2
D. m = 8
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
-
6
x
+
9
và 2 đường thẳng x 0; y 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 - 6 x + 9 và 2 đường thẳng x = 0; y = 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
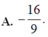
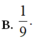
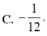
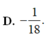
Các giá trị của tham số k để đường thẳng d: ykx cắt đồ thị hàm số
y
x
x
+
1
(
C
)
tại 2 điểm phân biệt là A. k
≠
0 B. k
≠
1 C. k 1 D. k ...
Đọc tiếp
Các giá trị của tham số k để đường thẳng d: y=kx cắt đồ thị hàm số y = x x + 1 ( C ) tại 2 điểm phân biệt là
A. k ≠ 0
B. k ≠ 1
C. k > 1
D. k ≠ 0 và k ≠ 1
Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
m
x
+
2
có hai điểm cực trị A và B và đường thẳng AB cắt đường tròn
x
-
1
2
+
y
-
1
2...
Đọc tiếp
Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A và B và đường thẳng AB cắt đường tròn x - 1 2 + y - 1 2 = 3 tại hai điểm phân biệt M, N sao cho khoảng cách MN lớn nhất
A. 1
B. 2
C. 5
D. Vô số
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. {0} B. R C. {-3} D. (-3; +∞).
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. {0}
B. R
C. {-3}
D. (-3; +∞).
Cho đồ thị C: y 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là A.
k
9
8
k
≠
0
B.
k...
Đọc tiếp
Cho đồ thị C: y= 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
A. k < 9 8 k ≠ 0
B. k > - 9 8 k ≠ 0
C. k < - 9 8 k ≠ 0
D. k > 9 8 k ≠ 0
Cho hàm số
y
x
-
x
+
1
có đồ thị, đường thẳng (d): y mx-m-1 và điểm A(-1;0) Biết đường thẳng d cắt đồ thị tại hai điểm phân biệt M, N mà
AM
2
+
AN...
Đọc tiếp
Cho hàm số y = x - x + 1 có đồ thị, đường thẳng (d): y = mx-m-1 và điểm A(-1;0) Biết đường thẳng d cắt đồ thị tại hai điểm phân biệt M, N mà AM 2 + AN 2 đạt giá trị nhỏ nhất. Mệnh đề nào dưới đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.