Đáp án B
Phương pháp giải: Tính đạo hàm, áp dụng điều kiện để hàm số nghịch biến trên khoảng
Lời giải: Ta có
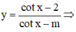
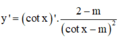
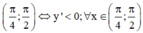 (*)
(*)
Mà 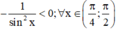 suy ra (*)
suy ra (*) 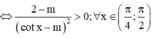
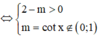
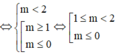
Vậy 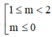 là giá trị cần tìm
là giá trị cần tìm
Đáp án B
Phương pháp giải: Tính đạo hàm, áp dụng điều kiện để hàm số nghịch biến trên khoảng
Lời giải: Ta có
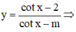
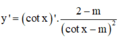
 (*)
(*)
Mà 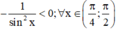 suy ra (*)
suy ra (*) 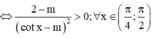
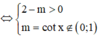
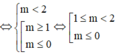
Vậy 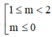 là giá trị cần tìm
là giá trị cần tìm
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m - sin x cos 2 x nghịch biến trên khoảng [0;π/6]?
A. 1.
B. 0.
C. 2.
D. Vô số.
Có tất cả bao nhiêu giá trị nguyên của tham số m Î [-20;20] để hàm số y = 8 c o t x + m - 3 . 2 c o t x + 3 m - 2 đồng biến trên khoảng (π/4;π)?
A. 10
B. 12
C. 11
D. 9
Tìm tất cả các giá trị thực của tham số m để hàm số y = cosx + m cosx − m nghịch biến trên π 2 , π .
A. − 1 < m < 0
B. m ≥ 0
C. m ≤ − 1
D. − 1 ≤ m ≤ 0
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x + m c o s x - m nghịch biến trên π 2 ; π
A. m ≤ - 1
B. -1 < m < 0
C. - 1 ≤ m ≤ 0
D. m ≥ 0
Gọi S là tập hợp tất cả các giá trị nguyên của m trên đoạn - 10 ; 10 để hàm số y = 8 c o t x + m - 3 2 c o t x + 3 m - 2 đồng biến trên π 4 ; π . Số phần tử của S là
A. 2
B. 8
C. 1
D. 7
Tìm các giá trị của m để hàm số y = 2 - x - 2 2 - x - m nghịch biến trên khoảng (-1; 1)
A. m ≤ 1 2 , m > 2
B. m ≤ 1 2
C. m > 2
D. m ≤ 2
Tìm tất cả các giá trị của m để hàm số y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 nghịch biến trên R.
A. - 1 < m ≤ 2
B. m ≤ - 1 m ≥ 2
C. - 1 ≤ m ≤ 2
D. - 1 ≤ m < 2
Có bao nhiêu giá trị nguyên của m ϵ (-15;15) sao cho hàm số y = tan x - 10 tan x - m đồng biến trên khoảng (0;π/4)?
A. 20
B. 9
C. 10
D. 29
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = - 1 3 x 3 – ( m + 1 ) x 2 + ( 4 m - 8 ) x + 2 nghịch biến trên toàn trục số
A. 9
B. 7
C. vô số
D. 8