Đáp án C
Em có:
lim x → a + g x = − ∞ ⇒ lim x → a + − g x = + ∞
⇒ lim x → a + f x − g x = lim x → a + f x + lim x → a + − g x = + ∞ ⇒ 1 đúng.
lim x → a + f x g x = − 1 ⇒ 2 đúng.
lim x → a + f x + g x không xác định => sai.
Đáp án C
Em có:
lim x → a + g x = − ∞ ⇒ lim x → a + − g x = + ∞
⇒ lim x → a + f x − g x = lim x → a + f x + lim x → a + − g x = + ∞ ⇒ 1 đúng.
lim x → a + f x g x = − 1 ⇒ 2 đúng.
lim x → a + f x + g x không xác định => sai.
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Giả sử f(x) và g(x) là các hàm số bất kỳ liên tục trên và a, b, c là các số thực.
Mệnh đề nào sau đây sai?
A. ∫ a b f x d x + ∫ b c f x d x + ∫ a c f x d x = 0
B. ∫ a b c f x d x = c ∫ a b f x d x
C. ∫ a b f x g x d x = ∫ a b f x d x . ∫ a b g x d x
D. ∫ a b f x - g x d x + ∫ a b g x d x = ∫ a b f x d x
Cho hàm số f ( x ) = x + x 2 2 + x 3 3 + . . . + x n + 1 n + 1 , n ∈ N . Tính lim x → ∞ f ' ( 1 3 ) .
A. L = 2 3
B. L = 3 2
C. L = 5 4
D. L = 7 4
Giả sử f(x) và g(x) là hai hàm số bất kỳ liên tục trên ℝ và a, b, c là các số thực. Mệnh đề nào sau đây sai?
A. ∫ a b f ( x ) d x + ∫ b c f ( x ) d x + ∫ a c f ( x ) d x = 0
B. ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
C. ∫ a b f ( x ) g ( x ) d x = ∫ a b f ( x ) d x . ∫ a b g ( x ) d x
D. ∫ a b f ( x ) - g ( x ) d x + ∫ a b g ( x ) d x = ∫ a b g ( x ) d x
Cho lim x → ∞ f x + 2 = 1 .Tính lim x → ∞ f x
A. lim x → ∞ f x = 3
B. lim x → ∞ f x = -1
C. lim x → ∞ f x = -3
D. lim x → ∞ f x = 1
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số f x = a x + b cx + d với a,b,c,d là các số thực và c ≠ 0 Biết f 1 = 1 , f 2 = 2 và f f x = x với mọi x ≠ - d c Tính lim x → ∞ f x
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Giới hạn lim x → 2 + x 2 - 2 x 2 - x bằng - m , m 0. Giá trị
biểu thức A = m2 - 2m là:
A . - 1
B . - 2
C .8
D . 1
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
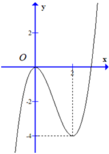
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1