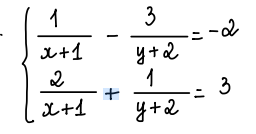\(\left\{{}\begin{matrix}\dfrac{1}{x+1}-\dfrac{3}{y+2}=-2\\\dfrac{2}{x+1}+\dfrac{1}{y+2}=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{6}{y+2}=-4\\\dfrac{2}{x+1}+\dfrac{1}{y+2}=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y+2}=7\\\dfrac{2}{x+1}+\dfrac{1}{y+2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y+2}=\dfrac{7}{7}=1\\\dfrac{2}{x+1}=3-1=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y+2=1\\x+1=\dfrac{2}{2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-2=-1\\x+1=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=0\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
,
3
x
+
4
,
2
y
1
9
x
+
14...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 , 3 x + 4 , 2 y = 1 9 x + 14 y = 4
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
x
-
2
y
10
x
-
2
3
y
3...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 x - 2 y = 10 x - 2 3 y = 3 1 3
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
4
x
+
7
y
16
4
x
-
3
y
-
24
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 4 x + 7 y = 16 4 x - 3 y = - 24
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
x
+
y
3
2
x
-
y
7
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3 x + y = 3 2 x - y = 7
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
10
x
-
9
y
8
15
x
+
21
y
0
,...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 10 x - 9 y = 8 15 x + 21 y = 0 , 5
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
+
2
3
y
5
3
2
x
-...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x + 2 3 y = 5 3 2 x - 3 y = 9 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
5
x
3
+
y
2
2
x
6
-...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5 x 3 + y = 2 2 x 6 - y 2 = 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
+
3
y
-
2
3
x
-
2
y...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x + 3 y = - 2 3 x - 2 y = - 3
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x
2
-
3
y
1
2
x
+
y
2...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: x 2 - 3 y = 1 2 x + y 2 = - 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
2
x
-
11
y
-
7
10
x
+
11
y...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x - 11 y = - 7 10 x + 11 y = 31