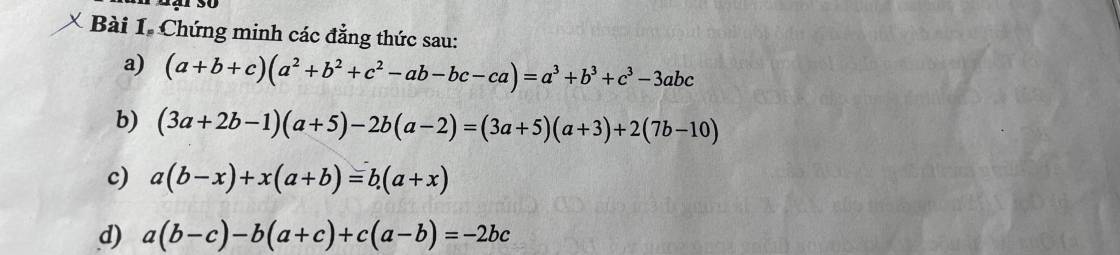\(M=\left[\left(3a+b+2c\right)^3-\left(3a\right)^3\right]-\left[b^3+\left(2c\right)^3\right]\\ M=\left(b+2c\right)\left[\left(3a+b+2c\right)^2+3a\left(3a+b+2c\right)+9a^2\right]-\left(b+2c\right)\left(b^2-2bc+4c^2\right)\\ M=\left(b+2c\right)\left(27a^2+9ab+6bc+12ac\right)\\ M=3\left(b+2c\right)\left(9a^2+3ab+2bc+6ac\right)\\ M=3\left(b+2c\right)\left(3a+2c\right)\left(3a+b\right)\)
Thế vào đề ta được \(m=3;n=3;p=2\)
Vậy \(mnp=3\cdot3\cdot2=18\)