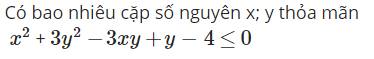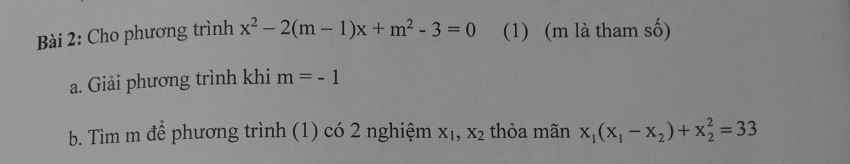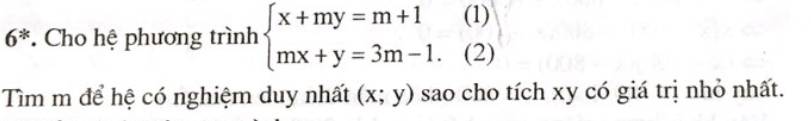Nhân 2 vế giả thiết với \(\sqrt{x^2+3}-x\)
\(\left(\sqrt{x^2+3}-x\right)\left(\sqrt{x^2+3}+x\right)\left(\sqrt{y^2+3}+y\right)=3\left(\sqrt{x^2+3}-x\right)\)
\(\Leftrightarrow\sqrt{y^2+3}+y=\sqrt{x^2+3}-x\) (1)
Tương tự, nhân 2 vế giả thiết với \(\sqrt{y^2+3}-y\) và rút gọn:
\(\Rightarrow\sqrt{x^2+3}+x=\sqrt{y^2+3}-y\) (2)
Cộng vế (1) và (2):
\(\Rightarrow\sqrt{x^2+3}+\sqrt{y^2+3}+x+y=\sqrt{x^2+3}+\sqrt{y^2+3}-x-y\)
\(\Leftrightarrow2\left(x+y\right)=0\)
\(\Leftrightarrow x+y=0\)




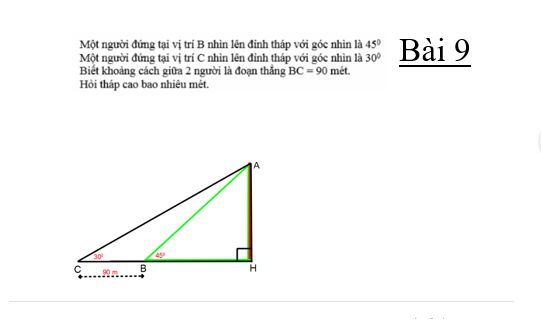 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ