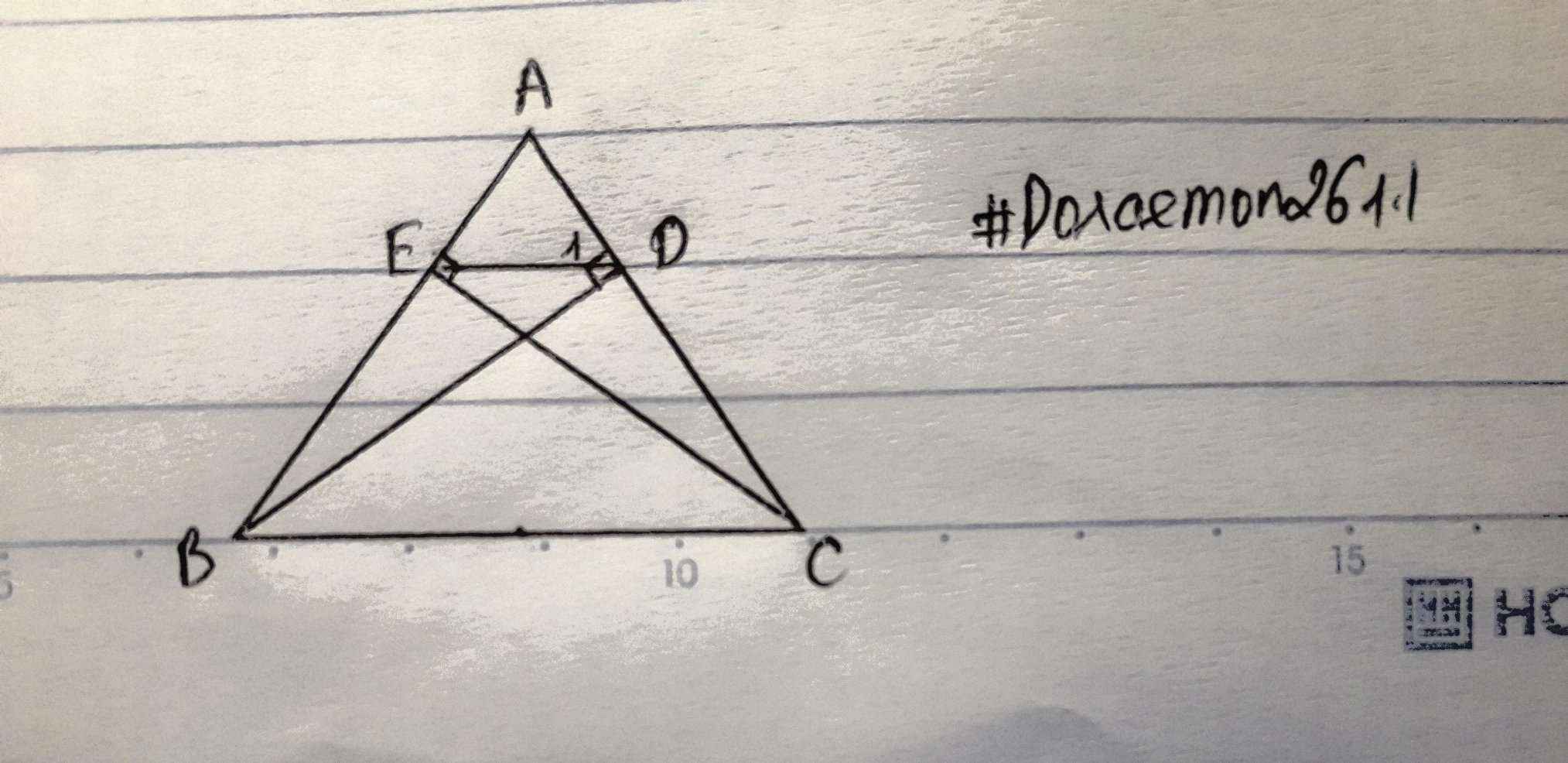
Xét `\triangle ADB` và `\triangle AEC` có:
`{:(\hat{ADB}=\hat{AEC}(=90^o )),(\hat{A} chung):}}=>`
`=>\triangle ADB` $\backsim$ `\triangle AEC` (g-g)
`=>[AD]/[AE]=[AB]/[AC]`
`=>[AB]/[AD]=[AC]/[AE]`
Xét `\triangle AED` và `\triangle ACB` có:
`{:([AB]/[AD]=[AC]/[AE]),(\hat{A} chung):}}=>`
`=>\triangle AED` $\backsim$ `\triangle ACB`
`=>\hat{D_1}=\hat{ACB}` (Mà `2` góc nằm ở vị trí đồng vị)
`=>ED //// BC=>` T/g `BCDE` là hình thang
Mà `\hat{EBC}=\hat{DCB}` (`\triangle ABC` cân tại `A`)
`=>` T/g `BCDE` là hình thang cân
`->Đpcm`










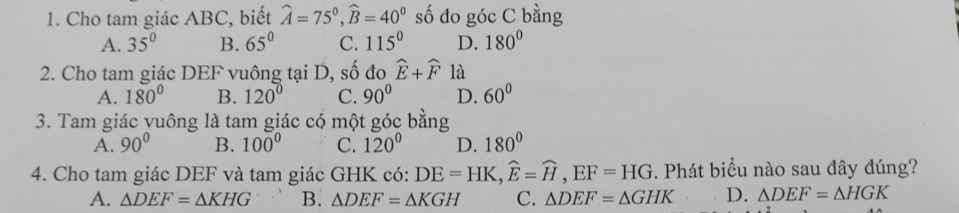



 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ
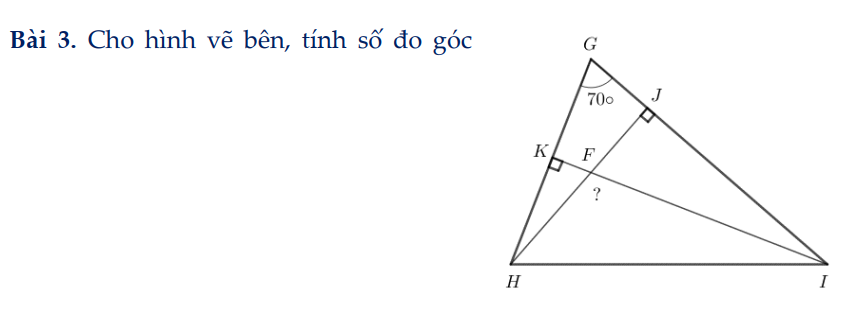 cần gấp
cần gấp




 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 
