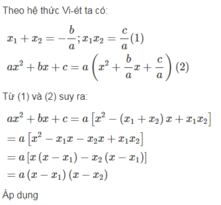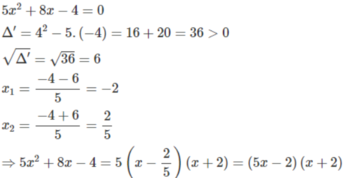Các câu hỏi tương tự
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
5 x 2 - (1 + 2 3 )x - 3 + 3
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
x 2 - 11x + 30
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
3 x 2 + 14x + 8
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
Chứng tỏ rằng nếu phương trình
a
x
2
+
b
x
+
c
0
có nghiệm là
x
1
v
à
x
2
thì tam thức
a
x
2
+
b
x
+...
Đọc tiếp
Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
phân tích đa thức thành nhân tử (với a b x y không âm, a> b)
a) xy - \(y\sqrt{x}\) + \(\sqrt{x}-1\)
b) \(\sqrt{ab}-\sqrt{by}+\sqrt{bx}+\sqrt{ay}\)
c) \(\sqrt{a+b}+\sqrt{a^2+b^2}\)
d) 12 - \(\sqrt{x}\) - x
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) 0b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.d) Chứng minh rằng phương trình bậc hai:(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) 0 luôn có hai nghiệm phân biệt.
Đọc tiếp
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.
Tìm tất cả các tam thức bậc hai hệ số nguyên f(x)=ax2+bx+c và g(x)=(a+1)x2+(b+1)x +(c+1) sao cho cả hai đều có nghiệm nguyên