Các câu hỏi tương tự
đối với những bài tìm đồng biến nghịch biến của hàm số, khi nào nên kẻ bảng biến thiên còn khi nào thì ko
mình hỏi riêng vì thấy có những bài có kể ko kẻ bảng biến thiên vẫn giải được nhưng đáp án vẫn kẻ
tại sao khi tính đạo hàm của hàm số để xét tính đồng biến, nghịch biến
một số trường hợp , lời giải xét y' >0,
trong khi số khác lại xét y' ≥ 0
Khoảng nghịch biến của hàm số y= 1/2x^4-3x^2-3 là gì các bạn?
Hàm số y= x^2/1-x đồng biến trên khoảng nào?
Hàm số y= x^3+3x^2 nghịch biến trên khoảng nào?
Cho hàm số y f(x) liên tục trên
ℝ
{1} và có bảng biến thiên như sau: Đồ thị hàm số
y
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng? A. 1 B. 2 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ \{1} và có bảng biến thiên như sau:
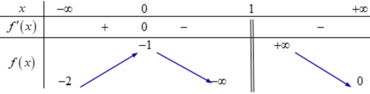 Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
A. 1
B. 2
C. 0
D. 2
Xét sự biến thiên của hàm số y sinx - cosx. Trong các kết luận sau, kết luận nào đúng? A. Hàm số đã cho đồng biến trên khoảng (
-
π
4
;
3
π
4
) B. Hàm số đã cho đồng biến trên khoảng (
3
π
4
;
7
π
4
) C. Hàm s...
Đọc tiếp
Xét sự biến thiên của hàm số y = sinx - cosx. Trong các kết luận sau, kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
Xét sự biến thiên của hàm số y sinx - cosx. Tìm kết luận nào đúng? A. Hàm số đã cho đồng biến trên khoảng (
-
π
4
;
3
π
4
) B. Hàm số đã cho đồng biến trên khoảng (
3
π
4
;
7
π
4
) C. Hàm số đã...
Đọc tiếp
Xét sự biến thiên của hàm số y = sinx - cosx. Tìm kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
Cho hàm số u(x) liên tục trên đoạn [0;5] và có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên m để phương trình
3
x
+
10
-
2
x
m
.
u
(
x
)
có nghiệm trên đoạn [0;5]? A. 6 B. 4 C. 5 D. 3
Đọc tiếp
Cho hàm số u(x) liên tục trên đoạn [0;5] và có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên m để phương trình 3 x + 10 - 2 x = m . u ( x ) có nghiệm trên đoạn [0;5]?
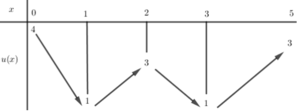
A. 6
B. 4
C. 5
D. 3
Xét sự biến thiên của hàm số y 1 - sinx trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai? A. Hàm số đã cho nghịch biến trên khoảng (
-
π
2
; 0) B. Hàm số đã cho nghịch biến trên khoảng (0;
π
2
) C. Hàm số đã cho đồng biến trên khoảng (
π
2
; π) D. Hàm số đã cho nghịch biến trên khoảng (
π...
Đọc tiếp
Xét sự biến thiên của hàm số y = 1 - sinx trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?
A. Hàm số đã cho nghịch biến trên khoảng ( - π 2 ; 0)
B. Hàm số đã cho nghịch biến trên khoảng (0; π 2 )
C. Hàm số đã cho đồng biến trên khoảng ( π 2 ; π)
D. Hàm số đã cho nghịch biến trên khoảng ( π 2 ; 3 π 2 )
Cho hàm số y 4sin(x +
π
6
) cos(x -
π
6
) - sin2x. Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho? A. Hàm số đã cho đồng biến trên các khoảng (0;
π
4
) và (
3
π
4
; π) B. Hàm số đã cho đồng biến trên (0; π). C. Hàm số đã cho nghịch biến trên khoảng (0;...
Đọc tiếp
Cho hàm số y = 4sin(x + π 6 ) cos(x - π 6 ) - sin2x. Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?
A. Hàm số đã cho đồng biến trên các khoảng (0; π 4 ) và ( 3 π 4 ; π)
B. Hàm số đã cho đồng biến trên (0; π).
C. Hàm số đã cho nghịch biến trên khoảng (0; 3 π 4 )
D. Hàm số đã cho đồng biến trên khoảng (0; π 4 ) và nghịch biến trên khoảng ( π 4 ; π)





